P1 de Física B - FIS1026 da PUCRIO - 2015.1

A posição de um objeto medida por um observador , relativa a um sistema de coordenadas, é dada por . A posição deste mesmo objeto medida por um observador , relativa a outro sistema de coordenadas é dada por .

a) Mostre que a aceleração do objeto é a mesma medida por ambos observadores.

b) Determine os vetores posição e velocidade medidos pelo observador , relativos ao observador .

Considere a situação ilustrada abaixo onde os dois blocos estão ligados por uma corda que passa por uma polia. O bloco 1 tem massa e o bloco 2 tem massa . As massas da polia e da corda podem ser consideradas como sendo desprezíveis. Existe atrito em todas as superfícies e o coeficiente de atrito cinético é igual a 0,40. Uma força é aplicada no bloco 1 de tal forma que os blocos se deslocam com velocidade constante, o bloco 1 para à direita e o bloco 2 para à esquerda.

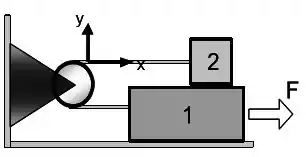
a) Faça o diagrama de corpo livre para o sistema e indique nos dois blocos, se existirem, as forças que formam pares ação-reação.

b) Escreva, na forma literal, as equações de movimento para o sistema. Resolva o sistema de equações e substitua os valores do enunciado para encontrar o vetor força . Utilize o sistema de coordenadas indicado.

Um passageiro de massa sentado em uma roda gigante se move com velocidade constante em uma trajetória circular de raio no plano vertical no sentido horário. Suponha que durante todo o movimento o passageiro está sempre sentado de cabeça para cima.

a) Faça um diagrama de corpo livre das forças que agem no passageiro no topo e no fundo da trajetória.

b) Escreva uma expressão literal para a diferença das forças normais que agem no passageiro nas duas posições. Como varia esta diferença em função da velocidade da roda gigante?

c) Suponha agora que no instante em que o passageiro alcança sua altura máxima, a força que age no assento aponta para baixo na direção vertical e tem módulo igual à do peso do passageiro. Para um raio igual a , calcule em quanto tempo a roda gigante dá uma volta completa.

Três blocos de massa , e estão conectados por cordas ideais através de uma polia ideal, apoiados em superfícies inclinadas de ângulos e como mostrado na figura. As massas dos blocos valem , , , , , e . Os valores dos coeficientes de atrito estático e cinético entre o bloco 1 e seu plano inclinado são respectivamente e .

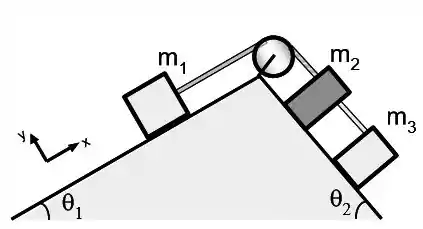
a) Faça um diagrama de corpo livre de cada bloco no espaço abaixo. Usando as leis de Newton, determine o valor da força de atrito estático sobre o bloco 1 para que o sistema permaneça em repouso. Não existe atrito entre os blocos 2 e 3 e o plano inclinado no qual estão apoiados.

b) Considere agora que o bloco 3 sofra a ação de uma força para baixo paralela ao plano inclinado que põe o sistema em movimento. Após certo momento, a ação dessa força cessa. Nesse instante o sistema de blocos está descendo o plano inclinado com velocidade de módulo . A partir desse instante obtenha o valor da aceleração do bloco 1.

c) Calcule a força de tração da corda sobre o bloco 1 durante a aceleração do ítem ().