Trabalho e Energia Cinética, Corpos Rígidos, Rotação, Dinâmica de Rotação, Momento Angular
Um aro uniforme de raio e massa está preso a um fio de massa desprezível e está girando em uma superfície horizontal. Na figura abaixo, a trajetória do centro de massa do aro está indicada pela circunferência tracejada. A trajetória tem raio e a velocidade angular do aro é . Suponha inicialmente que não há atrito entre o aro e a superfície.
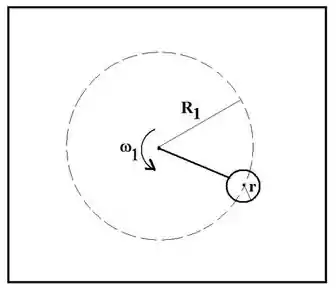
Escreva o módulo do momento angular do aro em relação ao centro da trajetória.
Um dispositivo oculto no centro da trajetória diminui o raio para . Neste novo raio, qual é o novo valor da velocidade angular ? Justifique claramente o conceito
físico utilizado.
Encontre o trabalho realizado pelo dispositivo oculto da letra b.
Suponha agora que há atrito entre o aro e a superfície. Se no instante o aro está girando na circunferência de raio (original) e com velocidade angular , e que o coeficiente de atrito estático é e o de atrito cinético é , calcule o intervalo de tempo que o aro demora em parar totalmente.
Passo 1
Para calcular o módulo do momento angular, precisamos da seguinte definição,
Vamos primeiro achar o momento de inércia do sistema, para isso lembre-se o teorema dos eixos paralelos! Vamos lá!
Agora podemos achar o módulo do momento angular:
Substituindo os valores:
Passo 2
Para determinar a nova velocidade angular, deveremos usar a lei da conservação do momento angular! Nesse caso, o momento angular se conserva, pois o torque resultante externo é zero. No sistema só atuam a força peso e a normal, cujos torques se anulam! Agora sim, vamos usar a lei!
Substituindo os valores, temos:
Passo 3
Pelo teorema do trabalho e energia cinética, temos:
Para o nosso sistema, só temos energia de rotação:
Substituindo os valores, temos:
Passo 4
Sabendo que a segunda lei de newton para a rotaçãoo nos diz que a taxa de variação do momento angular do sitema é igual a soma vetorial dos torques resultantes, temos:
Como os torques a força peso e da normal se anulam, teremos somente o torque exercido pela força de atrito cinético!
Como no fim o sistema para, teremos o momento angular depois igual a zero:
Isolando a variação de tempo e substituindo os valores, temos:
Resposta