P3 de Física B - FIS1026 da PUCRIO - 2015.2

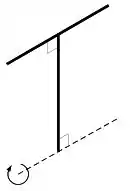
Parte I: Duas hastes iguais muito finas de comprimento e massa estão coladas em forma de um conforme ilustra a figura. O momento de inércia rotacional do conjunto em torno do eixo tracejado é:

(a)

(b)

(c)

(d)

(e) nenhuma das respostas acima.

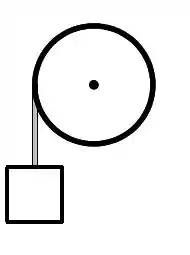
Parte II: Uma corpo de massa está conectado a uma corda que está firmemente enrolada em um cilindro de massa e raio . No instante abaixo o cilindro gira com velocidade angular e o corpo desce com velocidade de módulo igual a . A corda não desliza sobre o cilindro. Despreze a massa da corda e atritos. O módulo do momento angular do conjunto em relação ao centro do cilindro é:

(a)

(b)

(c)

(d)

(e) nenhuma das respostas acima.

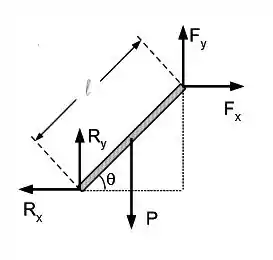
Parte III: Seja uma barra de comprimento e peso sobre a qual agem as forças ilustradas ao lado. O módulo do torque resultante em torno da extremidade superior é:

(a)

(b)

(c)

(d)

(e) nenhuma das respostas acima.

Após sofrer um impulso, um aro de massa e raio rola sem deslizar plano acima. O plano está inclinado de em relação à horizontal. No instante de tempo o aro tem velocidade angular de módulo e está na posição a partir da origem. Suponha que o plano é suficientemente longo e que o aro alcança sua altura máxima a uma distância . Após parar momentaneamente o aro rola sem deslizar plano abaixo. Utilize para a aceleração da gravidade e o sistema de eixos indicado.

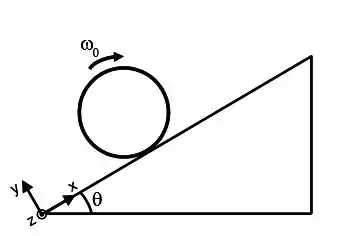
(a) Determine o momento de inércia rotacional do aro em relação ao ponto de contato com o plano inclinado.

(b) Determine a distância em função dos dados do problema.

(c) Determine o torque da força de atrito em torno do centro do aro, quando ele estiver momentaneamente parado, prestes a rolar sem deslizar plano abaixo.

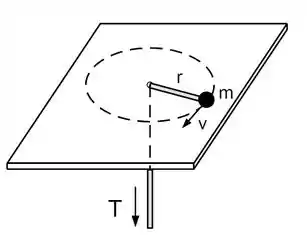
Um pequeno bloco de massa gira sobre uma superfície horizontal sem atrito e faz uma trajetória circular de raio com velocidade tangencial . O bloco está preso a uma corda de massa desprezível que passa por um furo no centro da superfície como mostra a figura. Num dado momento a corda é cuidadosamente puxada para baixo reduzindo o raio da trajetória do bloco para . Considere o bloco como uma partícula e responda:

(a) Durante o intervalo de tempo em que a corda é puxada, o momento angular do bloco em torno do furo é conservado? Justifique.

(b) Qual é a nova velocidade angular do bloco após a redução do raio da trajetória? Determine a variação de sua energia cinética.

(c) Determine a expressão literal que fornece o módulo da tensão no fio em função da massa , do raio e do momento angular em torno do furo.

(d) Seja a tensão máxima que o fio suporta igual a . Determine o raio da trajetória que o bloco percorre e a sua velocidade tangencial quando o fio estiver prestes a arrebentar.