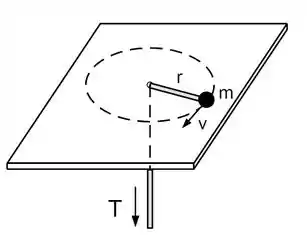
Um pequeno bloco de massa gira sobre uma superfície horizontal sem atrito e faz uma trajetória circular de raio com velocidade tangencial . O bloco está preso a uma corda de massa desprezível que passa por um furo no centro da superfície como mostra a figura. Num dado momento a corda é cuidadosamente puxada para baixo reduzindo o raio da trajetória do bloco para . Considere o bloco como uma partícula e responda:
(a) Durante o intervalo de tempo em que a corda é puxada, o momento angular do bloco em torno do furo é conservado? Justifique.
(b) Qual é a nova velocidade angular do bloco após a redução do raio da trajetória? Determine a variação de sua energia cinética.
(c) Determine a expressão literal que fornece o módulo da tensão no fio em função da massa , do raio e do momento angular em torno do furo.
(d) Seja a tensão máxima que o fio suporta igual a . Determine o raio da trajetória que o bloco percorre e a sua velocidade tangencial quando o fio estiver prestes a arrebentar.
Passo 1
(a) Sim, o somatório dos torques é zero. As forças que atuam no bloco são: Tensão, Peso e Normal. O torque em torno do furo das forças Normal e Peso se anulam. A Tensão não realiza torque, já que seu vetor aponta pro ponto de referência.
O que nos dá constante.
Passo 2
b) Como provamos que o se mantém constante:
Tratando o bloco como uma partícula:
Agora temos todos os dados para ter a variação de energia cinética:
Passo 3
(c)
Mas como , temos:
Passo 4
(d)
Quando fazemos a tensão ser máxima, o raio mínimo aparece na seguinte expressão:
Substituindo os valores:
Para achar a velocidade, vamos usar a conservação do momento angular:
Logo:
Resposta
a) Sim
b) ;
c)
d) ;