Uma escada homogênea está apoiada contra uma parede vertical sem atrito. O coeficiente de atrito estático entre a escada e o piso é . Qual é o menor ângulo entre a escada e a horizontal para que a escada não escorregue?
Passo 1
Temos o seguinte diagrama de forças para essa situação:
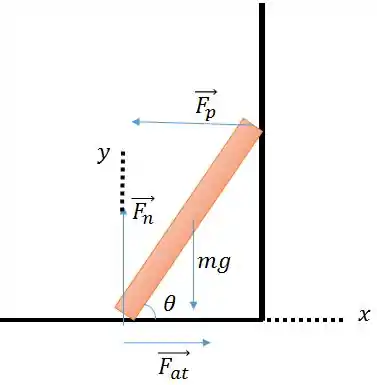
Queremos descobrir quanto vale o ângulo . Vamos lá?
Passo 2
Para a situação de equilíbrio, temos que:
Vamos aplicar esse somatório, tendo o ponto de contato da escada com o chão como referência. Sendo o comprimento da escada, temos:
Passo 3
Aora, vamos aplicar as demais condições de equilíbrio:
Ainda, temos que :
Logo:
Substituindo na fórmula do passo anterior, temos:
Logo:
Resposta
Exercícios de Livros Relacionados
Na Figura, uma prancha homogênea, com comprimento L de 6,10m e peso de 445N , repousa apoiada no chão e em um rolamento sem atrito no alto de uma parede de altura h=3,05m . A prancha permanece em equi
Uma caixa cúbica está cheia de areia e pesa 892N . Deseja-se "rodar" a caixa, empurrando horizontalmente uma de suas arestas superiores. (a) Qual é a força mínima necessária? (b) Qual é o coeficiente
Na figura, qual é o menor valor do módulo da força horizontal constante F aplicada horizontalmente ao eixo da roda que permite à roda ultrapassar um degrau de altura h = 3,00c m ? O raio da roda é r =
Uma escada, de massa desprezível e comprimento L , está apoiada contra uma parede lisa, formando um ângulo θ com o piso horizontal. O coeficiente de atrito entre a escada e o piso é μ . Um homem sobe
Uma escada homogênea está apoiada contra uma parede vertical sem atrito. O coeficiente de atrito estático entre a escada e o piso é 0,30 . Qual é o menor ângulo entre a escada e a horizontal para que