Uma escada de massa apoia-se numa parede vertical numa região onde a aceleração da gravidade é constante. A extremidade superior da escada está a uma altura do chão, e a distância da extremidade inferior da escada à parede também é . (veja a figura abaixo). Na situação I, não existe atrito entre a escada e a parede, mas existe atrito entre a escada e o chão. Já na situação II, existe atrito entre a escada e a parede, e também entre a escada e o chão. Onde há atrito, temos um coeficiente de atrito estático dado por , sendo . Em ambas as situações (I e II), a escada encontra-se em equilíbrio estático, mas está na eminência de escorregar. Nestas circunstâncias, calcule:
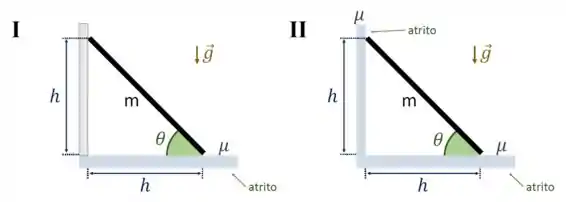
(a) O valor do coeficiente de atrito estático na situação I.
(b) O valor do coeficiente de atrito estático na situação II.
Passo 1
Letra : Primeiramente, vamos lembrar quais de equilíbrio sobre um corpo rígido. Para um corpo rígido estar em equilíbrio estático, duas condições devem ser satisfeitas: a soma vetorial de todas as forças sobre o corpo deve ser nula e a soma vetorial de todos os torques aplicados pelas forças com relação a um ponto de rotação qualquer deve ser nula. Matematicamente,
sendo , com o vetor que vai do ponto de rotação até o ponto onde a força foi aplicado e o produto vetorial que segue a regra da mão direita.
Desta forma, no próximo passo, vamos determinar as forças que atuam na escada. Simbora!
Passo 2
Neste passo determinaremos as forças que atuam na escada. Considere o digrama de corpo livre da escada dado abaixo.
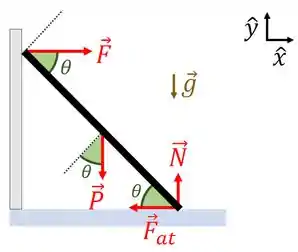
A força é a força peso da escada aplicada no meio da escada. A força é a força de atrito entre o chão e a escada. A força é a força normal que é reação da escada empurrar a parede para a esquerda. Já a força é a normal que é reação da escada empurrar o chão para baixo.
Vamos aplicar a primeira condição de equilíbrio. Desta forma, temos
Decompondo na direção dos versores e , temos que
Destas duas equações, temos que
Precisamos determinar . Faremos isso no próximo passo aplicando a segunda condição de equilíbrio. Bora galera!
Passo 3
Neste passo, aplicaremos a segunda condição de equilíbrio. Vamos analisar a figura abaixo.
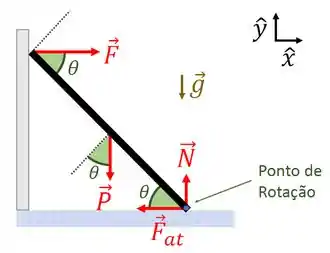
Adotaremos o ponto de rotação como sendo onde a escada toca o chão. Desta forma, note que o torque referente às forças de atrito e a normal de contato entre a escada e o chão são nulos (pois as forças estão sendo aplicadas sobreo o ponto de rotação). Deste modo, a segunda condição de equilíbrio nos retorna
com e e os vetores e dados na figura abaixo.
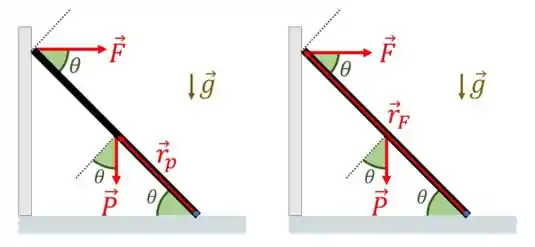
Todas as forças são coplanares (pertencem ao mesmo plano). Portanto, ao aplicarmos a regra da mão direita para o produto vetorial, temos que
sendo o menor ângulo entre os vetores e e o menor ângulo entre os vetores e .
Podemos relacionar os ângulos e com o ângulo . Para isso, veja a figura abaixo.
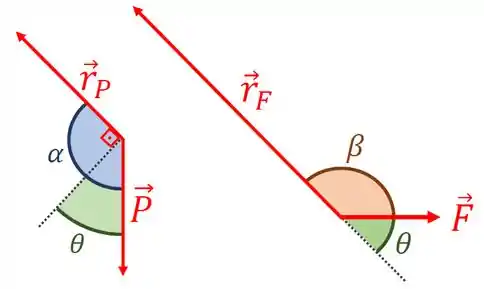
Assim, como e são os menores ângulos, temos imediatamente que
Logo,
Temos também que os módulos dos vetores e são dados por
sendo o comprimento da escada.
Deste modo, temos que a segunda condição de equilíbrio retorna
Vamos substituir a expressão na expressão para no próximo passo.
Passo 4
Mostramos no passo 2 que é dado por
Desta forma, utilizando o resultado do passo 3, temos que
Precisamos determinar . Considere a figura abaixo.
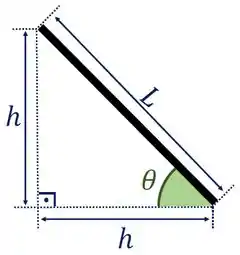
Desta forma, vemos imediatamente que
Portanto, na situação I, temos que
Passo 5
Letra : Para resolver esse item nós basicamente faremos da mesma forma que no item (a). Então vamos mais rápido para gente não perder tempo. As forças na escada agora são as seguintes.
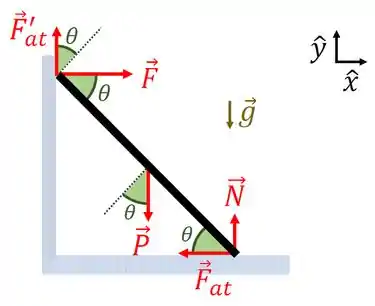
A única força nova que aparece devido ao atrito da escada com a parede é . Assim, a primeira condição de equilíbrio nos retorna
Decompondo na direção dos versores e , temos que
Destas duas equações, temos que
Precisamos determinar . Para tanto, aplicaremos a segunda condição de equilíbrio. Tomando o mesmo ponto de rotação do item (a), temos que
sendo que , pois as forças e são aplicadas no mesmo ponto.
Assim, aplicando a regra da mão direita nos produtos vetoriais, temos que
com e dados como no item (a) e dado na figura a seguir.
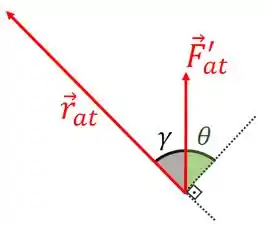
Vemos imediatamente que . Deste modo, temos
Desta forma, sabendo que , e , temos que
Agora podemos substituir na equação para . Faremos isso no próximo passo.
Passo 6
Mostramos no passo 5 que
Substituindo uma equação na outra, dá para mostrar que
Assim, o valor de satisfaz a equação do 2º grau anterior. As raízes dessa equação são
O enunciado diz que . Portanto, a única raiz fisicamente aceitável é. Portanto, para a situação II, o valor de é