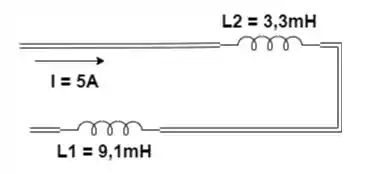
Calcule a energia armazenada no circuito de indutores abaixo:
Passo 1
Primeiro devemos calcular a indutância equivalente. Como as duas indutâncias estão em série:
Passo 2
A fórmula da energia armazenada num indutor é:
Resposta
Exercícios de Livros Relacionados
Em t=0, a tensão em um capacitor de 25 mF é 10 V. Calcule a tensão do capacitor para t0 quando a corrente 5t mA passa através dele.
A corrente em um indutor de 200 mH é i = (B1 cos 200t + B2 sen 200t)e-50t A, t $ 0. A tensão no indutor (convenção passiva) é 4,25 V em t = 0. Calcule a potência nos terminais do indutor em t = 25 ms.
Considere o circuito da figura 6.84. Dado que v t = 12 e - 3 tm V para t0 e i 1 0 = - 10 m A , determine: a i 2 0 ; b i 1 tei 2 t .
No circuito da figura 6.82, i_o (0) = 2 A . Determine i_0 (t) e v_0 (t) para t0 .
Indutores em paralelo podem ser associados da mesma forma que resistores em paralelo.VerdadeiroFalso