Determine , e a energia armazenada no capacitor e indutor no circuito abaixo em condições de CC.
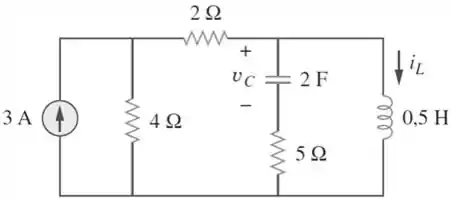
Passo 1
Como a gente viu o capacitor em CC é um circuito aberto e o indutor é um curto-circuito. Então, vamos redesenhar o circuito.
Passo 2
A corrente só circula em caminhos fechados. Logo, ela não passa pelo resistor de e a tensão e a corrente podem ser obtidas conforme no circuito abaixo:
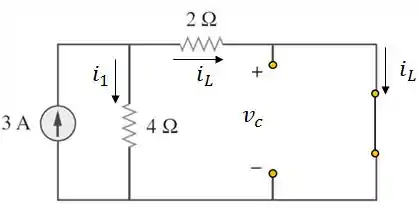
Tá lembrado de divisor de corrente? Vamos usar aqui:
Passo 3
Aplicando a lei de Ohm, temos:
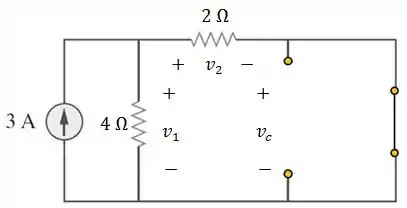
Aplicando a LTK:
Passo 4
Agora que já calculamos e , vamos calcular a energia armazenada nos elementos.
Primeiro no capacitor:
Agora no indutor:
Resposta
Exercícios de Livros Relacionados
Em t=0, a tensão em um capacitor de 25 mF é 10 V. Calcule a tensão do capacitor para t0 quando a corrente 5t mA passa através dele.
A corrente em um indutor de 200 mH é i = (B1 cos 200t + B2 sen 200t)e-50t A, t $ 0. A tensão no indutor (convenção passiva) é 4,25 V em t = 0. Calcule a potência nos terminais do indutor em t = 25 ms.
Considere o circuito da figura 6.84. Dado que v t = 12 e - 3 tm V para t0 e i 1 0 = - 10 m A , determine: a i 2 0 ; b i 1 tei 2 t .
No circuito da figura 6.82, i_o (0) = 2 A . Determine i_0 (t) e v_0 (t) para t0 .
Indutores em paralelo podem ser associados da mesma forma que resistores em paralelo.VerdadeiroFalso