Verifique que, para todo par de pontos tem-se:

(Dica: use o Teorema do Valor Médio)

Beleza. Agora que temos o teorema, podemos tentar conectar com o que foi pedido. A função no caso é a tangente, como podemos perceber pelo enunciado. E o intervalo seria .

Só que tem um detalhe importante. Repare que o intervalo do teorema é fechado , isto é, quer dizer que é um conjunto que inclui os números e . Já o intervalo do problema é aberto , isto é, não inclui os números e .

Com bons motivos! Porque a tangente desses números tende ao infinito! Ou seja, não daria pra pôr na fórmula algo do tipo

Beleza, só nos resta pensar um intervalo fechado qualquer para atacar a questão. Inclusive fica parecido com o que eles querem . Aplicando o teorema, existe tal que:

Calculando a derivada:

Portanto, temos:

Agora basta analisar o que ele quer. Basicamente, se arrumarmos o enunciado, usando a álgebra, podemos ver o que realmente eles querem:

Colocando ele com a cara daquela parada que achamos no fim do passo vamos precisar passar dividindo para esquerda, então vamos ter

Ele basicamente quer que a expressão que nós achamos para a derivada seja maior ou igual a um, portanto ele quer que:

Mas isso já é um fato no intervalo estudado! Vamos simplesmente mostrar isso.

Temos que, no intervalo em questão:

Basta olhar o círculo trigonométrico:

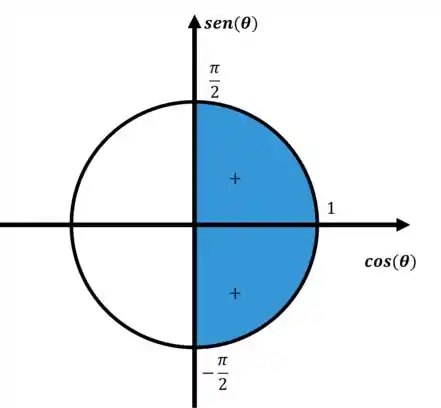
Já o inverso do cosseno, pelas propriedades de desigualdades:

Ainda pelas propriedades de desigualdades, se elevarmos a função ao quadrado:

Portanto, temos:

-

Substituindo de volta na expressão:

Pegando o módulo em ambos os lados:

Isolando:

C.Q.D. (Como queríamos demonstrar).