Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integração de Romberg

Ver Teoria
Exercício 3124567

Enunciado

Utilize o conteúdo aprendido para realizar o primeiro passo da Integração de de Romberg para obter uma aproximação para a integral abaixo com k = 1,2 , 3   .

I = ∫ 0 π s e n x d x

Passo 1

Vamos determinar os termos R k , 1 :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 1,1 = h k 2 f a + f b

Para k = 1 :

R 1,1 = ( b - a ) 2 f a + f b

R 1,1 = ( π - 0 ) 2 s e n ( π ) + s e n ( 0 )

R 1,1 = 0

Passo 2

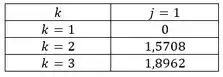
Para k = 2 :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 2,1 = 1 2 [ R 1,1 + h 1 . f a + h 2 ]

h k = b - a 2 k - 1

h k = b - a 2

R 2,1 = 1 2 [ R 1,1 + b - a . f a + b - a 2 ]

R 2,1 = 1 2 [ 0 + π - 0 . s e n 0 + π - 0 2 ]

R 2,1 = 1 2 [ π . s e n π 2 ]

R 2,1 = π 2 = 1,5708

Passo 3

Para k = 3 consideramos :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 3 , 1 = 1 2 { R 2 , 1 + h 2 . [ f a + h 3 + f a + 3 . h 3 ]

R 3,1 = 1 2 { R 2,1 + h 2 . [ f a + h 3 + f a + 3 . h 3 ]

h 3 = b - a 2 k - 1 = b - a 4

R 3,1 = 1 2 { R 2,1 + b - a 2 . f a + b - a 4 + f a + 3 . b - a 4 }

R 3,1 = 1 2 { R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4 }

R 3,1 = 1 2 { R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4 }

R 3,1 = 1 2 { 1,5708 + π 2 . f π 4 + f 3 . π 4 }

R 3,1 = 1 2 { 1,5708 + π 2 . s e n π 4 + s e n 3 . π 4 }

R 3,1 = 1,8962

Resposta