Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução a testes de aderência

Ver Teoria
Exercício 312456

Enunciado

Passo 1

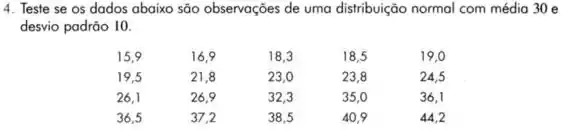
Neste exercício precisamos testar a hipótese se as probabilidades observadas são próximas das probabilidades esperadas, e faremos isso, pelo teste de aderência. Aqui precisaremos primeiro definir quem são as categorias, para assim encontraramos o número de casos esperados para cada uma das categorias.

Passo 2

Vamos dividir os possíveis resultados nos quartils teóricos da Normal(30,100), Q(0,25), Q(0,5) e Q(0,75), chamaremos Z(p), os quantis da N(0,1)

Q 0,25 = 30 + 10 Z 0,25 = 30 + 10 - 0,6745 = 23,255

Q 0 , 5 = 30 + 10 Z 0 , 5 = 30 + 10 0 = 30

Q 0,7 5 = 30 + 10 Z 0,7 5 = 30 + 10 0,6745 = 3 6 , 745

Passo 3

Agora vamos olhar para a tabela e ver quantos valores estão em cada um dos intervalos:

(-∞; 23,255] = 8 = O1

(23,255; 30] = 4 = O2

(30; 36,745] = 4 = O3

(36,745; +∞) = 4 = O4

Os valores esperados de uma normal esperam que em cada quartis temos a mesma quantidade de valores, como n=20 e são 4 quartis

E i = 5   p a r a   t o d o   i = 1,2 , 3,4

Passo 4

Agora vamos aplicar os dados na estatística de teste:

X 2 = ∑ i = 1 s ( O i - E i ) 2 E i

X 2 = ( 8 - 5 ) 2 5 + ( 4 - 5 ) 2 5 + ( 4 - 5 ) 2 5 + ( 4 - 5 ) 2 5

X 2 = 1,8 + 0,2 + 0,2 + 0,2 = 2 , 4

Passo 5

Agora vamos achar na tabela da qui-quadrada o quantil 95% com 3 graus de liberdade

X 0,05,5 2 = 7,815

Passo 6

Comparando agora os dois valores encontrados temos que:

2,4 < 7,815

Logo a um nível de significância de 5% não rejeitamos H0, isto é, temos evidência que os dados seguem o modelo proposto.

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma indústria registra, em cada semana, o número de dias em que ocorrem acidentes de trabalho. Para uma amostra de 200 semanas, verifique se os dados apresentados a seguir, aderem ao modelo Binomial c
Utilizando a tabela da distribuição qui-quadrado determine (aproxime se necessário): P ( χ 7 214,70 ) P ( χ 23 239 ) P χ 12 2 ≤ 9 P ( 12χ 17 2 ≤ 30,2 ) O valor de a tal que P χ 13 2a = 0,05 O valor de
Para verificar a qualidade do processo de fabricação, cabos de aço são submetidos ao ensaio de tração até acontecer à ruptura. Os cabos têm 5 metros de comprimento e deseja-se testar se o modelo Unifo
Na tabela abaixo, X significa número de filhos homens em famílias com 12 filhos. Calcule para cada valor da variável o número de famílias que você deveria esperar se X ~ b ( 12 ; 0,5 ) .Você acha que
As tabelas a seguir contêm o número de pessoas segundo origem e opinião a respeito do aborto.Para cada sexo, verifique se origem e opinião são independentes.Combine as informações em uma única tabela