Considere os dados abaixo, que supostamente são uma amostra de tamanho de uma distribuição normal, de média e variância . Os dados já estão ordenados.
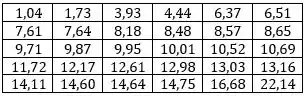
Ao nível de significância de , podemos afirmar que os dados se adequam a uma distribuição Normal?
Passo 1
Neste exercício precisamos testar a hipótese se as probabilidades observadas são próximas das probabilidades esperadas, e faremos isso, pelo teste de aderência. Aqui precisaremos primeiro definir quem são as categorias, para assim encontraramos o número de casos esperados para cada uma das categorias.
E essa parte pode parecer meio confusa, como assim definir categorias? Quem vão ser nossas categorias?
A verdade é que existem múltiplas respostas para essa pergunta. Uma forma que vai funcionar é a gente pensar nos quartis dos dados de uma distribuição.
Se dividirmos qualquer distribuição em 3 quartis principais, tipo o primeiro, o segundo, e o terceiro, esperamos que o número de dados entre cada um deles seja o mesmo né? Pois vamos pulando de em dos dados, sem alterar esse intervalo.
Então a ideia é a gente ver quantos elementos tem entre cada um desses quartis na distribuição da Normal citada, e depois verificar quantos dos dados observados cabem dentro de cada um desses quartis. Partiu?!
Passo 2
Para isso, vamos calcular o valor dos quartis primeiro. Como fazer isso? Usando a tabela da Normal padrão!
Na tabela da Normal padrão, nós encontramos os quartis dessa forma:
Já que a tabela nos da valores de probabilidades acumuladas até certo , esses vão ser justamente nossos quartis nesses casos. Procurando na tabela vemos que:
Agora, para descobrir os quartis REAIS, ou seja, os da distribuição , precisamos “despadronizar” os quartis da Normal padrão. Para isso, multiplicamos o valor deles pelo desvio padrão, e depois somamos a média (operações inversas da padronização):
Passo 3
Agora vamos olhar para a tabela dada e ver quantos valores estão em cada um dos intervalos:
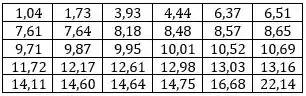
E os valores esperados para o número de elementos entre dos quartis principais de uma distribuição são iguais, ou seja, o valor que divide a distribuição em 4 partes iguais. Como :
Passo 4
Agora vamos aplicar os dados na estatística de teste:
Passo 5
Agora vamos achar na tabela da qui-quadrada o quantil 95% com 3 graus de liberdade
Passo 6
Comparando agora os dois valores encontrados temos que:
Logo a um nível de significância de 5% não rejeitamos H0, isto é, temos evidência que os dados seguem o modelo proposto.
Resposta
Ei, a resposta está no passo a passo :)