Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução às EDO's

Ver Teoria
Exercício 5123467

Enunciado

USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 3

Assinale a alternativa correspondente à solução do sistema de equações diferenciais.

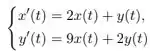
satisfazendo a condição   x ( 0 ) �� =   0 ,   y ( 0 )   =   6 :

  1.   x ( t )   =   - e - t   +   e 5 t ,   y ( t )   =   3 e - t +   3 e 5 t
  2. x ( t )   =   0 ,   y ( t )   =   6 e 5 t  
  3. x ( t )   =   0 ,   y ( t )   =   6 ;  
  4. x ( t )   =   e t   -   e - t ,   y ( t )   =   2 e t   +   4 e - t
  5. x ( t )   =   2 e - t   -   2 e 5 t ,   y ( t )   =   6 e - t

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez queremos resolver um sistema de EDO

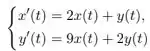
com a seguinte condição inicial

  x ( 0 )   =   0 ,   y ( 0 )   =   6

Como fazemos?

A primeira coisa que precisamos fazer é escrever o sistema em forma matricial, e depois obter os autovalores e autovetores da matriz do sistema. Então temos que

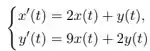
pode ser representado como

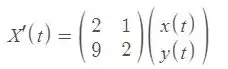
Onde X ' ( t ) = ( x ' ( t ) , y ' ( t ) ) T

calculando o polinômio característico dessa matriz, chegamos em

p ( x ) = ( 2 - x ) 2 - 9

Logo, como os autovalores são as raízes desse polinômio temos que os autovalores serão:

- 1   e   5

E quais são os autovetores associados?

Por definição, o autovetor associado ao autovalor a é tal que

A v = a v

No nosso caso, A é matriz do sistema de EDO. Então,

A v = - v

⇒ v = ( 1 , - 3 )

E temos que

A v = 5 v

⇒ v = ( 1,3 )

Logo os autovetores associados aos autovalores - 1   e   5 são, respectivamente

( 1 , - 3 )   e   ( 1,3 )

Passo 2

Agora que temos os autovalores e autovetores. Podemos calcular a solução do sistema de EDO.

A solução de um sistema de EDO com autovalores reais distintos é dada por

X ( t ) = c 1 ( v 1 e a 1 t ) + c 2 ( v 2 e a 2 t )

onde c i ∈ R ,   a i é um autovalor e v i o autovetor associado ao autovalor a i . Dessa forma, a nossa solução geral fica

X ( t ) = c 1 ( ( 1 , - 3 ) e - 1 t ) + c 2 ( ( 1,3 ) e 5 t )

= c 1 ( e - 1 t , - 3 e - 1 t ) + c 2 ( e 5 t , 3 e 5 t )

= ( c 1 e - 1 t + c 2 e 5 t , - 3 c 1 e - 1 t + c 2 3 e 5 t )

Agora, precisamos encontrar as constantes c 1 e   c 2 . Podemos fazer isso pois temos a seguinte condição inicial

  x ( 0 )   =   0 ,   y ( 0 )   =   6

Como X ( t ) = ( x ( t ) , y ( t ) )

então

X ( 0 ) = ( x ( 0 ) , y ( 0 ) )

⇒ ( c 1 + c 2 , - c 1 3 + c 2 3 ) = ( 0,6 )

então temos que

c 1 + c 2 = 0

- c 1 3 + c 2 3 = 6

Logo, temos que

c 1 = - 1

c 2 = 1

Ou seja, a solução do sistema de EDO é

( - 1 e - 1 t + 1 e 5 t , + 3 e - 1 t + 3 e 5 t )

valor presente na alternativa a )

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a)