Em um experimento sobre reflexão e refração com luz linearmente polarizada, verifica-se que a luz incidente é totalmente refratada quando posicionada no ângulo de incidência de entre dois meios.
Qual a razão entre o índice de refração do meio inicial , pelo índice de refração do meio do feixe refratado .
Passo 1
Para a luz ser totalmente refratada, significa que por algum motivo não tem luz sendo refletida.
O motivo é que a luz é linearmente polarizada. Quando ela reflete no ângulo de polarização, a luz refletida é completamente polarizada perpendicular ao plano de incidência (plano formado pelos raios refletido – se ele existisse – refratado e incidente).
Se a luz incidente não tiver nenhum componente nessa direção, então não veremos nenhuma luz refletida. É isso que está ocorrendo aqui.
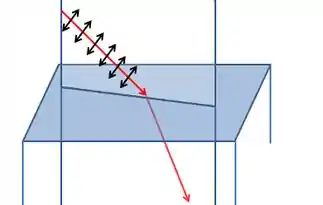
O problema então é encontrar a razão entre o índice de refração dos meios a partir do ângulo de polarização que nesse caso é , pois é medido em relação a normal.
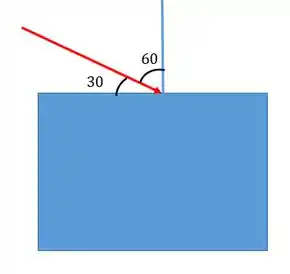
Passo 2
A lei de Brewster nos dá a relação entre a razão dos índices de refração e o ângulo de polarização.
Invertendo a equação, teremos:
Como o ângulo de polarização é , temos .
A resposta então é a letra b).
Resposta
Letra 1)