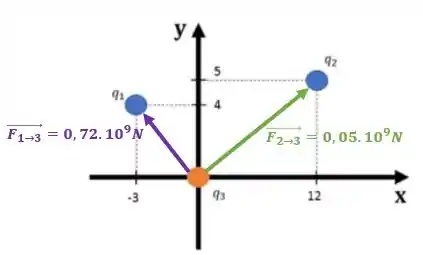
Dada a configuração de cargas abaixo:

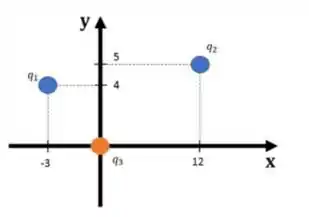
Onde:

Calcule e desenhe as forças aplicadas a carga .

Nesse caso, como temos mais de cargas, teremos uma força resultante na carga que depende da força que a carga fará na carga :

E da força que a carga fará na carga :

Da seguinte forma:

Vamos substituir os valores que foram dados no enunciado!

Vamos substituir a constante eletrostática :

Colocando nas equações, desejamos calcular apenas os módulos:

Agora substituindo as cargas:

Colocando nas equações:

Pensando em módulo, os valores negativos se tornam positivos

Agora vamos falar sobre as distâncias, olhando apenas para as cargas e :

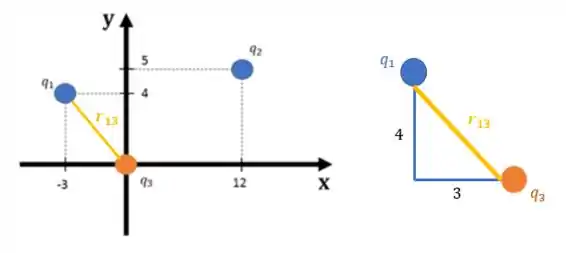
Veja que com as coordenadas, formamos um triângulo retângulo com a distância total entre as cargas e .

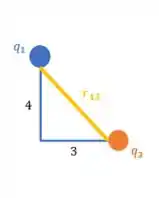
Através do Teorema de Pitágoras, sabemos que em um triângulo retângulo soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. Calma, eu vou te explicar quem é cada um, olha:

Os catetos são os lados do triângulo que formam um ângulo de , no nosso caso, eles são:

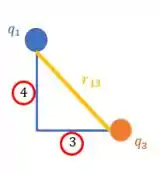
Enquanto a hipotenusa é o lado do triângulo oposto ao ângulo de 90°:

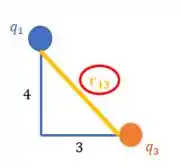
Então o Teorema de Pitágoras nos diz que:

Calculando essas parcelas ao quadrado:

Então a distância entre as cargas ao quadrado é igual a:

Essa distância ao quadrado é exatamente o que precisamos colocar na equação:

Pensando agora na distância entre a carga e a carga , temos:

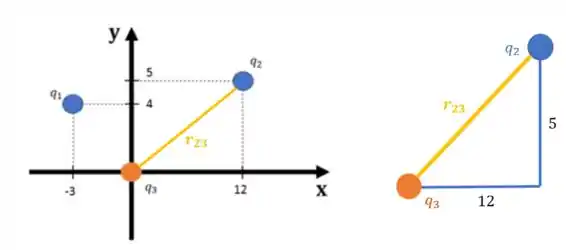
Aplicando o Teorema de Pitágoras, teremos a distância ao quadrado:

Então:

Aplicando na equação:

Vamos fazer esses cálculos:

Multiplicando os números e dividindo pelo denominador temos:

Então a primeira força é:

Isso é igual a:

Enquanto a multiplicação e a divisão da segunda força resultam em:

Então o módulo da segunda força será igual a:

Agora que sabemos os módulos das forças, como as cargas e são negativas, enquanto a carga é positiva, teremos que as duas forças que calculamos são atrativas:

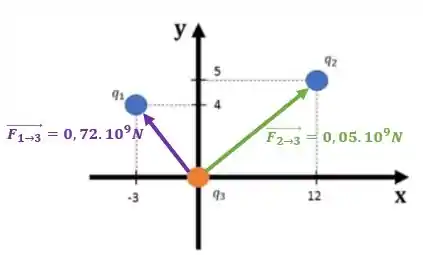
Percebe comigo que como a carga está mais distante, a força que ela aplica em é menor.