Dado um sistema isolado conforme discriminado abaixo:
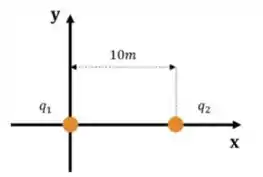
As cargas são dadas por: e .
Calcule a força elétrica que a partícula faz na e que a partícula faz na .
Dados:
Passo 1
Bom pessoal, vamos começar relembrando a fórmula da força elétrica em módulo:
A força elétrica depende das cargas elétricas e da distância entre elas.
Passo 2
Vamos substituir os valores que foram dados no enunciado!
Colocando na equação:
Agora a distância entre as cargas no gráfico é igual a metros:
Passo 3
Vamos calcular essa força:
Primeiro fazendo a divisão de potência. Como tem a mesma base, mantemos a base e subtraímos os expoentes:
Agora ficamos com:
Agora podemos multiplicar os números que não são potências
Tudo bem, chegamos no módulo da força!
Passo 4
Agora precisamos encontrar a direção e o sentido da força elétrica, pois ela é um vetor. Primeira coisa que podemos perceber é que como as duas cargas são positivas, elas se repelem:
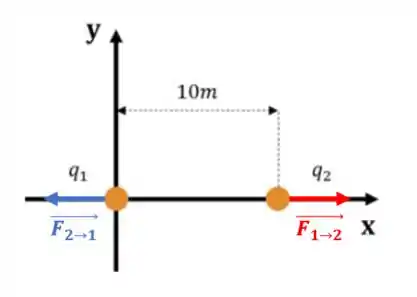
Ou seja, a força que a carga faz na carga , que chamamos de , empurra a carga para longe dela no sentido negativo do eixo . Usamos o vetor unitário para representar o sentido positivo do eixo . Como queremos o sentido negativo, precisamos colocar um sinal de menos
Enquanto, a força quea carga faz na carga , que chamamos de , empurra a carga para longe dela no sentido positivo do eixo :
Passo 5
Vamos então substituir o valor do módulo que encontramos:
Em:
e
Temos então:
e
Resposta final, pessoal!