Energia Potencial
Produzido por Pablo RicardoTeoria
Introdução
A maioria de nós já teve o desejo de atirar com arco e flecha, seja por influência de filmes ou jogos...

Mas você já parou para pensar como um arco e flecha funciona?
Para lançar a flecha, é preciso tirar o elástico da sua posição de equilíbrio e quanto mais você esticar o elástico mais longe sua flecha irá.
Isso porque ao esticar o elástico acumulamos uma energia que será convertida em movimento da flecha.
Neste tópico vamos estudar os tipos de energia associada aos movimentos dos corpos. Partiu?
Energia Potencial
Energia potencial nada mais é do que a capacidade que um corpo tem de realizar trabalho. Ela mede a quantidade de trabalho que uma força faz quando ela move um corpo da sua posição inicial até uma posição de referência.
Energia Potencial Gravitacional
Imagine um corpo que está a uma altura h com relação a uma referência:
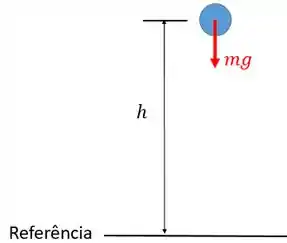
Esse corpo vai ter uma energia associada referente a sua altura com relação ao solo, a qual vamos chamar de energia potencial gravitacional :
Essa energia corresponde a capacidade da força peso de realizar trabalho fazendo o corpo retornar à linha de referência, pois na linha de referência a energia é zero .
Então não esqueça que energia potencial gravitacional está associada a uma certa altura de um corpo com relação ao referencial.
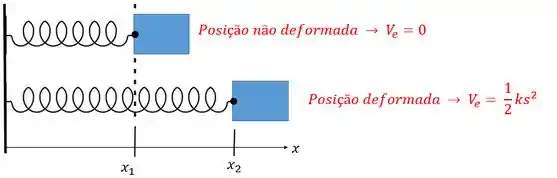
Energia Potencial Elástica
Quando puxamos ou comprimimos uma mola, ela sofre uma deformação. A energia potencial elástica é justamente a energia associada a essa deformação:
Energia potencial gravitacional generalizada
Para o caso em que as alturas são muito grandes ao ponto de serem comparáveis com o raio da Terra, não podemos usar a fórmula que vimos anteriormente. Nesses casos, devemos utilizar a seguinte fórmula:
Onde:
Raio da Terra.
Gravidade.
Massa do corpo.
Distância do centro da terra até o centro do corpo (é a nossa nova “altura”).
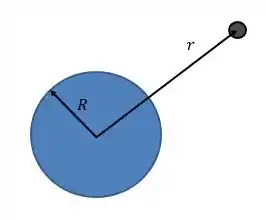
Assim:
Função Potencial
Se um corpo está submetido tanto a força gravitacional quanto elástica, a energia potencial desse corpo vai ser a soma das energias potenciais gravitacional e elástica. Vamos chamar essa soma de função potencial :
Equação Trabalho-Energia modificada
Agora vamos modificar a equação de trabalho-energia para acrescentar a contribuição da energia potencial:
Onde,
: Variação da energia cinética
: Variação da energia potencial
Podemos escrever assim:
Ou seja, a soma da variação da energia potencial gravitacional com a variação da energia potencial elástica. Podemos escrever assim também:
Mas quem será neste caso? Será a soma dos trabalhos das forças externas que são todas as forças que atuam em um corpo sem ser a força elástica nem a potencial. A atuação dessas últimas duas forças já está computada nas variações de energia potencial. ![]()
Então, por exemplo, se existir uma força de atuando no sistema, devemos calcular o trabalho dessa força e representá-lo como .
Mas você deve estar se perguntando quando que vai usar isso, né? Você usa quando não importar a trajetória que o corpo faz e sim o que acontece no início e no final.
Beleza! Vamos praticar fazendo os exercícios?
Energia Potencial
Energia Potencial Gravitacional
Energia Potencial Elástica
Energia potencial gravitacional generalizada
Função Potencial
Equação Trabalho-Energia modificada
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 132, 3/154
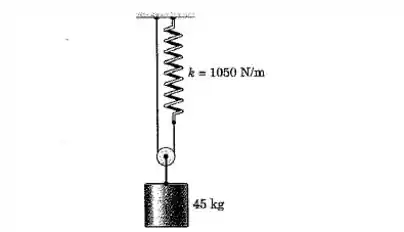
O sistema é liberado a partir do repouso com a mola inicialmente esticada em . Calcule a velocidade do cilindro após este ter caído . A mola tem uma rigidez de . Despreze a massa da pequena polia.
Passo 1
Vamos usar:
Como estamos lidando apenas com forças elásticas e gravitacionais:
Assim:
Passo 2
Assim:
Botamos um sinal de menos no último termo pois o enunciado disse que a massa “desceu”. Em outras palavras, a altura do ponto inicial é e a altura do ponto final é negativa.
Pelo enunciado, . Assim:
Temos:
Passo 3
Assim:
Resolvendo:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 131, 3/147
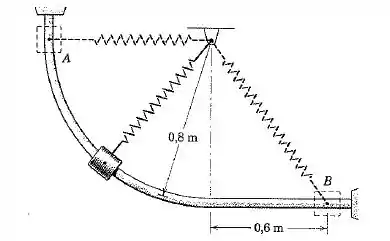
A mola tem um comprimento não esticado de e uma rigidez de . O Cursos de e a mola conectada são liberados a partir do repouso em e se deslocam no plano vertical. Calcule a velocidade do cursos quando este atinge na ausência de atrito.
Passo 1
Vamos usar, novamente:
Nesse caso, temos uma energia potencial e uma energia elástica. Assim;
Passo 2
Nesse problema, não existe a atuação de uma força externa, assim:
Podemos dizer, então:
Onde
A equação que escrevemos também pode ser escrita por:
Passo 3
A velocidade inicial é nula. Assim:
Considerando a altura inicial, altura em , igual a zero, podemos dizer que a variação de energia potencial gravitacional é negativa:
Perceba que a altura é o raio do ¼ de circunferência.
E a variação de energia potencial elástica?
Vamos ver.
Passo 4
Como:
Onde é o alongamento da mola, devemos calcular
Para os dois casos, o comprimento não esticado da mola vale
Em
E em
Bom, em você vai ter que calcular o comprimento de através do triângulo retângulo da figura. Assim:
Assim:
Então:
Passo 5
Assim:
Resolvendo:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 132, 3/152
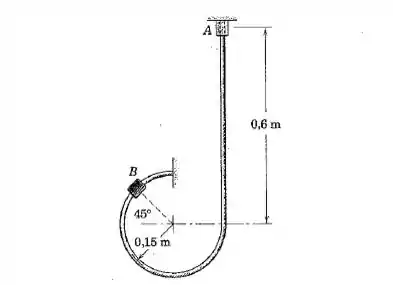
Um cursor com uma massa de é liberado a partir do repouso em e desliza para baixo e em torno do arame liso fixo. Determine a força entre o arame e o cursor quando este passa o ponto .
Passo 1
O sistema pode ser presentado por:
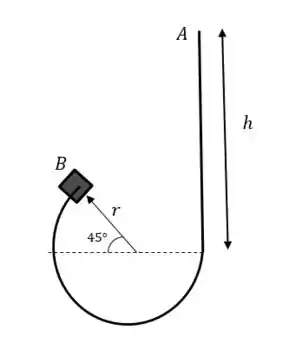
Vamos usar a seguinte fórmula:
No caso desse problema:
Assim:
Passo 2
Colocando a altura nula no centro do círculo, podemos dizer a variação da energia potencial gravitacional é dada por:
Passo 3
A variação da energia cinética é dada por:
Assim:
Vamos usar isso no próximo passo (:
Passo 4
As forças atuando na caixa serão:
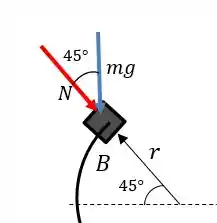
Como o corpo está rotacionando, teremos uma resultante centrípeta. Podemos escrever:
Assim, substituindo o :
Passo 5
Usando
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 136, 3/174
Um satélite artificial que se desoloca em uma órbita elíptica tem uma velocidade de a uma altitude de km no ponto . Determine sua velocidade no ponto onde a altitude é . Considere a Terra como uma esfera de raio e use para a aceleração da gravidade na superfície da Terra.
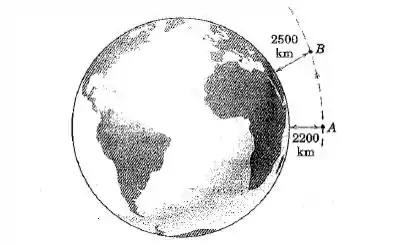
Passo 1
Aqui vamos usar a fórmula generalizada para a energia potencial gravitacional:
Onde é a distância até o centro da terra o próprio raio da terra.
Passo 2
Assim, a variação é dada por:
Assim:
Deixamos em função de porque não a conhecemos.
Passo 3
A variação de energia cinética será:
Perceba que estamos convertendo de para ali em cima.
Passo 4
Como não há forças externas, podemos dizer que:
Cortando os
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 134, 3/166
O cursor tem uma massa de e está preso à mola leve, que tem uma rigidez de e um comprimento sem deformação de . O cursor é liberado a partir do repouso em e desliza para cima na barra lisa sob a ação da força constante de . Calcule a velocidade do cursor quando este passa a posição .
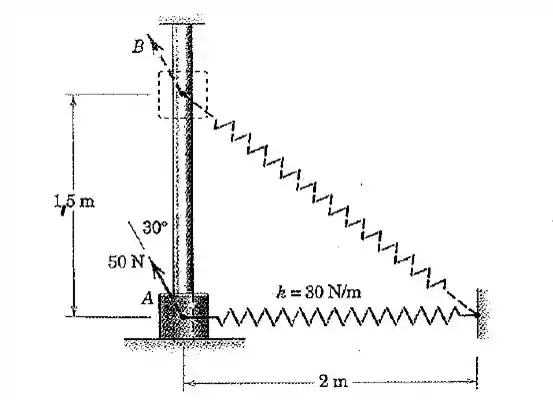
Passo 1
Podemos usar:
No caso desse problema, existe sim uma força externa que realiza trabalho. Esse trabalho é dado por:
Passo 2
A variação de energia cinética será dada por:
E a variação de energia potencial gravitacional? Assim:
Passo 3
A variação da energia elástica será:
Quanto vale ? é o alongamento da mola no final. Pra isso, precisamos calcular o comprimento da hipotenusa daquele triângulo do enunciado e depois subtrair disso o valor do comprimento da mola não esticada:
E ? Segue o mesmo princípio, só que para o ponto inicial:
Assim:
Passo 4
Assim:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 132, 3/151
O êmbolo de é liberado a partir do repouso na posição mostrada onde a mola de rigidez foi comprimida para a metade do seu comprimento sem deformação de . Calcule a altura máxima acima da posição inicial alcançada pelo âmbolo.
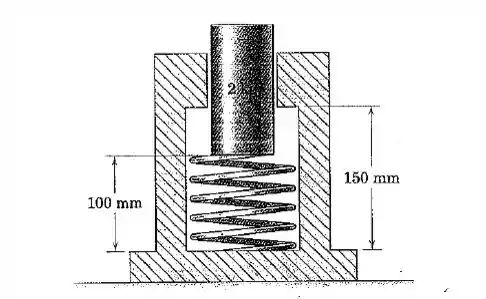
Passo 1
Podemos aplicar:
Porém, não existe força externa aplicada, assim:
Então:
Passo 2
No início e no final o êmbolo se encontra em repouso, assim:
Então:
Passo 3
Assim:
Só que:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 134, 3/165
Um satélite é colocado em uma órbita elíptica em torno da Terra e tem uma velocidade na posição do perigeu . Determine a expressão para a velocidade na posição do apogeu . Os raios para e são, respectivamente, e . Observe que a energia total permanece constante.
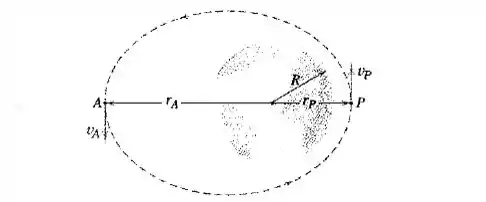
Passo 1
Como a única força atuante é a força gravitacional, podemos dizer:
Passo 2
Assim: