Impulso e Quantidade de Movimento
Produzido por Pablo RicardoTeoria
Fala aí! Seja muito bem vindo ao Responde Aí! Hoje a gente vai aprender sobre Impulso e quantidade de movimento!
O que é Impulso?
Quando seu carro enguiça, por exemplo, e é preciso empurrá-lo até que ele entre em movimento, você precisa dar aquele impulso, né? Então, o que é esse impulso?
O impulso
-Beleza, mas como eu posso calcular o impulso?!
Impulso: Fórmula
Pra a gente calcular o impulso é muito simples! É só multiplicar a força
Note que o impulso é um vetor que sempre tem a mesma direção e sentido da força .
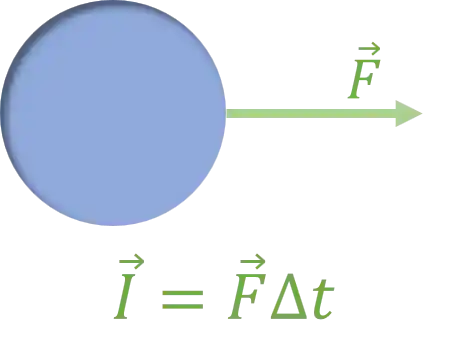
Mas e se a força não for constante ao longo do tempo? Neste caso, temos que integrar:
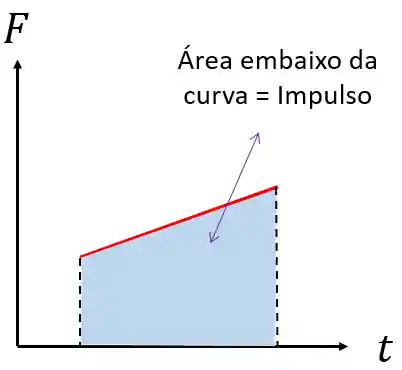
Outra forma de calcular o impulso quando a força for variável é pela área do gráfico de força por tempo
📢 Clique para saber mais:
- Impulso e Quantidade de Movimento Angular;
- Impulso e Quantidade de Movimento Linear: Exercícios Resolvidos
- Dinâmica: Aulão Salva-Vidas
Quantidade de Movimento
A quantidade de movimento
Nesse vídeo aqui em baixo a gente explica tudo o que você precisa saber sobre Impulso e Quantidade de movimento, pra arrasar na prova! 👇
Quantidade de Movimento: Fórmula
E como fazemos para calcular a quantidade de movimento!? É só multiplicar a massa
Repare que a quantidade de movimento é um vetor que vai sempre ter a mesma direção e sentido do vetor velocidade.

A quantidade de movimento também pode ser chamada de momento linear e sua unidade no SI é
Conservação da Quantidade de Movimento
Quando dois corpos colidem, dizemos que há conservação da quantidade de movimento. Por quê? Porque as colisões ocorrem muito rapidamente, então podemos desprezar qualquer ação de forças que poderiam causar impulsos.

Dessa forma temos a seguinte igualdade:
Embora a conservação da quantidade de movimento ocorra, não necessariamente isso é verdade em relação à energia cinética E. Então, temos os seguintes casos:
Se
- Se
colisão inelástica.
Teorema Impulso-Quantidade de Movimento
Agora podemos entender qual é a relação entre impulso e quantidade de movimento!
De acordo com o teorema impulso-quantidade de movimento o impulso exercido por um corpo é igual a sua variação de quantidade de movimento. Matematicamente temos:
Se abrirmos as fórmulas do impulso e da quantidade de movimento ficaria assim:
Tanto o impulso quanto a quantidade de movimento são vetores, então podemos abrir essa expressão e fazer as contas usando as componentes de cada eixo, caso você não queira trabalhar com vetores:
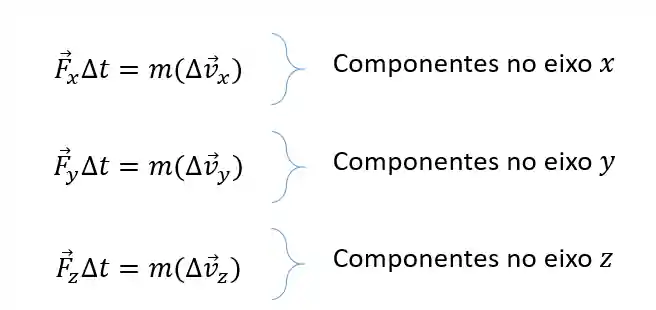
Diagrama Impulso–Quantidade de Movimento
Neste diagrama vamos fazer três desenhos e ele vai ser muito útil para nos ajudar a não esquecer nenhuma força. Vamos ver o passo a passo para a sua construção. Pra começar, imagine um corpo onde esteja atuando uma força
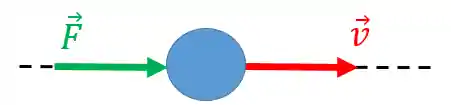
Primeiro, vamos olhar só para as forças que atuam no corpo. Temos que isolar o elemento principal e colocar só o vetor impulso na mesma direção e sentido do vetor força:
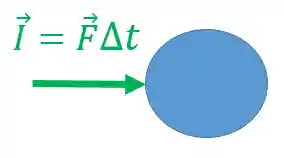
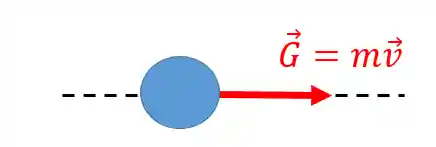
Neste segundo desenho vamos olhar só o vetor velocidade. Temos que isolar o corpo e colocar só o vetor quantidade de movimento na mesma direção e sentido do vetor velocidade:
E finalmente vamos olhar para a situação final. Vamos supor que a bolinha bateu em algum lugar e está com um movimento na direção contrária. Neste caso, temos que fazer um diagrama semelhante ao primeiro, ou seja, vamos olhar só o novo sentido da velocidade e vamos calcular um novo vetor quantidade de movimento:
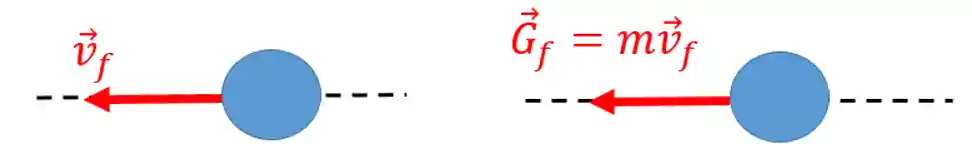
Agora, vamos ter:
Agora bora pros exercícios?!