Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 174
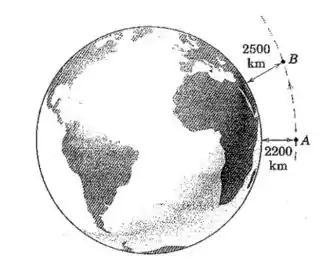
Um satélite artificial que se desloca em uma órbita eliptica tem uma velocidade de a uma altitude de no ponto . Determine sua velocidade no ponto onde a altitude é . Considere a Terra como uma esfera de raio e use para a aceleração da gravidade na superfície da Terra.
Passo 1
Pela conservação de energia temos:
Vamos encontrar fórmulas para cada um desses termos. Começando pela energia potencial:
E para facilitar podemos escrever isso em termos da aceleração da gravidade na superfície da Terra:
Onde é o raio da Terra.
Passo 2
A fórmula da variação da energia cinética é ainda mais simples:
Agora vamos substituir isso tudo na lei de conservação de energia:
E agora podemos dividir tudo por e substituir os valores:
Resposta
A velocidade no ponto é .
Exercícios de Livros Relacionados
A corrente de comprimento L é liberada a partir do repouso sobre o plano inclinado liso com x = 0 . Determine a velocidade v dos elos em termos de x .
A corrente inicia do repouso com um número suficiente de elos pendurados sobre a borda para apenas começar o movimento superando o atrito entre o restante da corrente e a superfície de apoio horizonta
O funicular é constituído por duas cabines de passageiros, cada uma com massa m , uma em cada extremidade do cabo de comprimento total L e massa ρ por uma unidade de comprimento. O sistema é operado p
As duas partículas de massa m e 2 m , respectivamente, estão conectadas por uma haste rígida de massa desprezível e deslizam com atrito desprezível em uma trajetória circular de raio r no interior do
O sistema é liberado a partir do repouso com a mola inicialmente esticada em 75m m . Calcule a velocidade v do cilindro após este ter caído 12m m . A mola tem uma rigidez de 1050N / m . Despreze a mas