Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 175
O cursor de é liberado a partir do repouso em e desliza para baixo na guia parabólica lisa (que está localizada em um plano vertical) sob a influência do seu próprio peso e da mola de constante . Determine a velocidade do cursor quando este passa o ponto e a força normal correspondente exercida pela guia sobre este. O comprimento sem deformação da mola é .
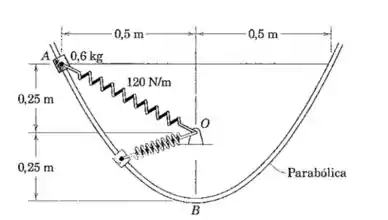
Passo 1
Vamos dizer que a energia potencial é nula na altura do ponto . Pela lei de conservação de energia temos:
Onde a energia potencial é a soma da gravitacional e da elástica:
E para calcular a energia elástica precisamos fazer a diferença entre o comprimento da mola nessa posição e o comprimento relaxado:
Agora vamos analisar a posição .
Passo 2
Agora vamos analisar as energias do ponto :
Passo 3
E agora vamos calcular a força normal no ponto mais baixo da trajetória. Vamos analisar a soma das forças voltadas para cima no ponto mais baixo:
E então:
Precisamos descobrir o raio de curvatura da trajetória. A fórmula de que precisamos é a seguinte:
Isso quer dizer que precisamos achar uma função que descreva aquela parábola. Se colocarmos a origem sobre o ponto , a função terá a seguinte forma:
E podemos pegar um ponto qualquer da parábola para determinar o valor de :
E então:
Agora podemos calcular o raio de curvatura:
Como o ponto em que estamos interessados é o ponto (a origem do nosso sistema), o raio é:
E substituindo na equação para a normal:
Resposta
A velocidade no ponto é e a força normal no ponto mais baixo da trajetória é .