Movimento Absoluto de Corpos Rígidos
Produzido por Pablo RicardoTeoria
Introdução
Você já jogou boliche? Já reparou no movimento que a bola faz?
Quando você joga a bola de boliche, ela rola até atingir os pinos. Para isso, ela tem que se deslocar na horizontal e ao mesmo tempo gira em torno do seu centro.
É este tipo de movimento que vamos estudar aqui. Quando um corpo realiza o movimento de rotação e de translação simultaneamente. Então vamos lá!
Movimento Absoluto
Agora vamos analisar o movimento de translação ocorrendo simultaneamente com a rotação. Ou seja, vamos trabalhar com as variáveis do movimento retilíneo junto com as variáveis angulares do movimento rotacional. Beleza?
Para começar, vamos pensar no movimento de translação e de rotação separadamente para facilitar nossa vida e depois arranjar um jeito de relacionar os dois.
Pense em um disco rolando pela superfície de uma mesa:
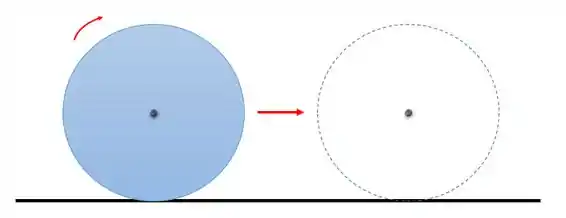
Vamos escolher duas referências que caracterizem o movimento do disco. Para isso, imagine que vamos pegar uma canetinha e marcar neste disco uma reta. Como o disco é um círculo é mais fácil escolhermos o seu raio. Vamos marcar o raio a partir do ponto de contato do disco com a mesa:
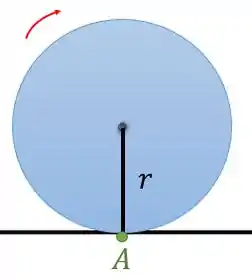
Quando o disco se mover, o que acontecerá com esta reta ?
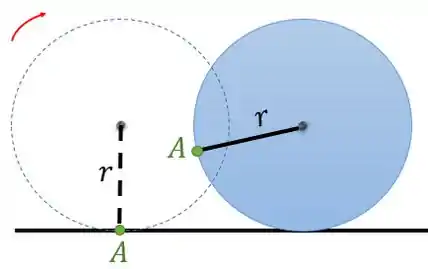
Repare que a reta girou conforme o disco foi rolando para a direita. Desse modo, podemos marcar a posição angular desta reta:
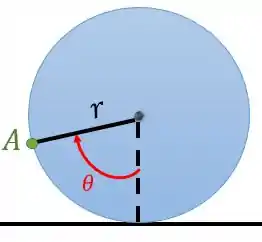
Ou seja, para analisar o movimento de rotação de um corpo vamos sempre marcar uma reta que pertença ao corpo.
E para o movimento de translação? Vamos pegar nossa canetinha e marcar um ponto no corpo. Como o disco é um círculo vamos escolher o seu centro:
Quando o disco rolar, o que vai acontecer com o ponto ?
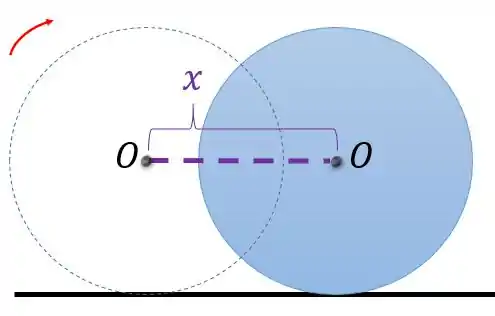
Repare que o ponto somente se deslocou em linha reta, ou seja, realizou um movimento de translação. Então, sempre que quisermos analisar o movimento de translação temos que marcar um ponto do corpo. Beleza?
Agora vem a sacada de mestre. Para resolver esse tipo de problema temos que arranjar um jeito de relacionar esses dois movimentos. E como vamos fazer isso? Usando trigonometria!!!
Vamos juntar os dois movimentos na mesma figura e tentar achar uma relação trigonométrica entre eles:
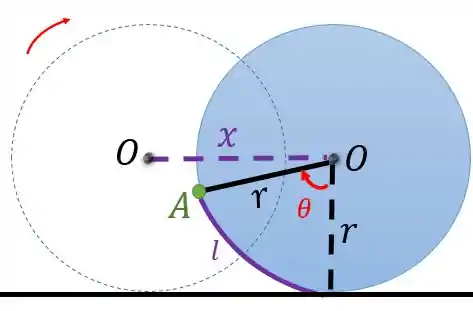
A medida que o disco rola para a direita, ele se desloca uma distância da sua posição inicial. Repare que a distância que ele deslocou na horizontal vai ser igual a quanto o disco rolou, ou seja, o comprimento do arco :
Mas sabemos que o comprimento do arco é calculado multiplicando o raio pelo ângulo :
Então, vamos ter que:
Esta equação nos dá a posição. Então, é só derivarmos com relação ao tempo para saber a velocidade:
Como o raio é constante, teremos que a velocidade é:
Mas lembra que a velocidade angular é:
Então, vamos substituir isso na equação da velocidade:
E a aceleração? É só derivarmos a equação da velocidade com relação ao tempo:
Aqui é só lembrar que a aceleração angular é:
Então, nossa aceleração será:
Ou seja, se pedirem a velocidade do disco é só usarmos essa equação aqui:
E se pedirem a aceleração vamos usar:
Beleza?
Mas essas equações só valem se o disco rolar sem deslizar, tá bom? Geralmente vai ter essa informação no enunciado.
Resumindo... Sempre que você tiver um corpo realizando rotação e translação ao mesmo tempo, é só seguir esse passo a passo:
- Marque uma linha no corpo para analisar o movimento de rotação;
- Marque um ponto no corpo para ver o que acontece na translação;
- Ache uma relação trigonométrica que relacione o ângulo de rotação com o deslocamento na horizontal;
- Derive a equação da posição para achar uma equação para a velocidade;
- Derive a velocidade para achar a equação da aceleração.
Então é isso aí. O mais difícil neste tópico é achar uma relação trigonométrica que relacione os dois movimentos. Só praticando exercícios mesmo para pegar o jeito. Partiu?
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 252-5/27
O cursor se desloca na ranhura horizontal com uma velocidade constante por um curto intervalo de movimento. Determine a velocidade angular da barra em termos do deslocamento .
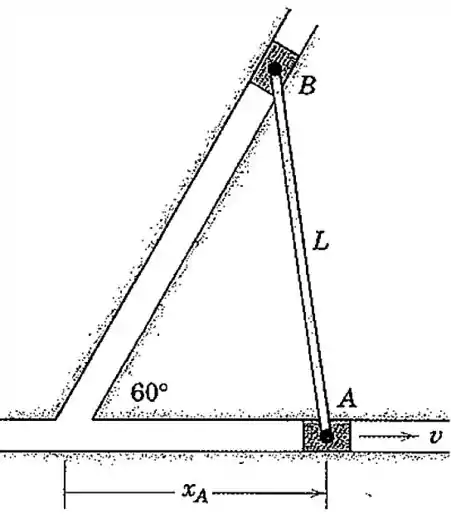
Passo 1
Nosso primeiro passo neste tipo de questão é achar uma relação trigonométrica que relacione a posição com a posição angular da barra .
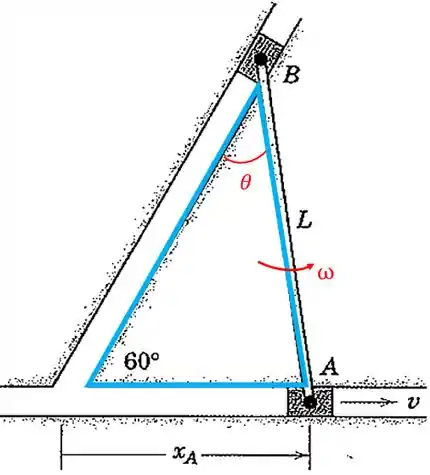
Repare que temos um triângulo formado dentro da figura:
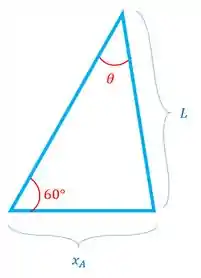
Vamos usar a lei dos senos para relacionar essas coisas:
Então a posição será:
Passo 2
Agora vamos achar a velocidade da barra . Para isso, é só derivarmos a equação da posição que acabamos de achar:
Repare que deixei tudo que é constante fora da derivada. Então, como o ângulo varia no tempo temos que aplicar a regra da cadeia:
Sabendo que
Então, teremos:
A barra está se movendo com uma velocidade constante e que foi chamada de , então:
A nossa equação da velocidade vai ficar:
Mas essa velocidade é dada no enunciado. O que queremos saber é a velocidade angular da barra . Então, vamos isolar na nossa equação:
Beleza?
Passo 3
Maaaas.... O enunciado pede a velocidade angular da barra em função de , ou seja, temos que arranjar um jeito de sumir com o ângulo e fazer surgir .
Lembra da lei dos senos que usamos lá no início do exercício? Vamos pegar aquela equação de volta:
Só que agora vamos isolar o e deixar tudo em função de :
Agora é só substituir isso na nossa equação da velocidade angular? Bem que poderia, mas lá não tem :
Tem apenas !!! Então, vamos pensar em uma relação trigonométrica que relacione seno e cosseno...
Agora sim!!! Vamos isolar o nessa relação aí:
Mas sabemos que o nosso é:
Então, vamos substituir esse valor de na nossa relação que acabamos de montar:
Vamos ter que:
Agora sim podemos substituir o na equação da velocidade angular:
Então, nossa equação da velocidade angular da barra é:
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 260-16.33
A barra gira uniformemente em torno do eixo em com velocidade angular constante . Determine a velocidade e a aceleração da barra que é obrigada pelas guias a se mover verticalmente.
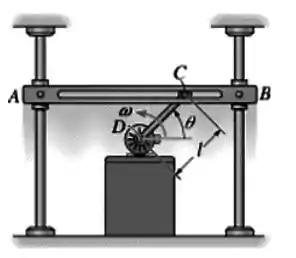
Passo 1
Primeiro vamos entender o que está acontecendo: a barra está girando em torno do ponto e conforme o ângulo aumenta a barra sobe.
A questão pede a velocidade e aceleração do movimento vertical da barra . Ou seja, temos que arranjar um jeito de relacionar o ângulo com a posição vertical da barra .
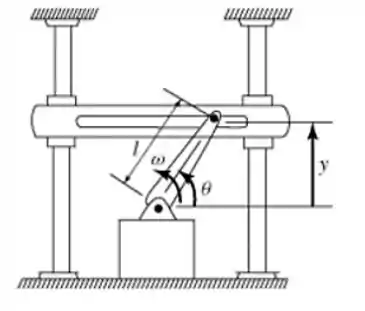
Repare que temos o seguinte triângulo retângulo:
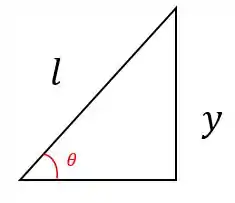
Para relacionar com o ângulo é só usarmos o seno:
Essa é a equação da posição da barra . Beleza?
Passo 2
Mas queremos saber a velocidade, não é mesmo? Então vamos derivar essa equação que achamos:
Como o comprimento da barra é constante, então:
Como o ângulo varia no tempo, para resolver esta derivada temos que aplicar a regra da cadeia:
Mas lembra que a velocidade angular é:
Então:
Passo 3
Agora falta a aceleração. Vamos derivar a equação da velocidade:
Vamos ter que aplicar a regra do produto e a regra da cadeia:
Temos que lembrar que:
E:
Vamos substituir na nossa equação:
Vamos dar uma ajeitada nisso:
Mas repare que no enunciado foi dito que a barra gira uniformemente em torno do ponto , ou seja, seu velocidade angular é constante. Portanto, a aceleração angular é zero:
Então, a nossa equação fica:
É isso aí!
Resposta
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 252-5/29.
O ponto recebe uma aceleração constante para a direita a partir do repouso com essencialmente nulo. Determine a velocidade angular da barra em termos de e .
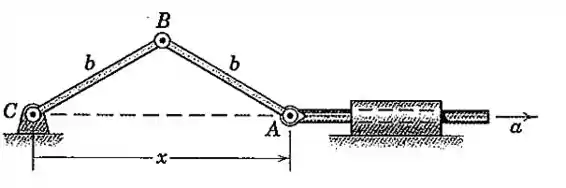
Passo 1
Nosso primeiro passo é arranjar um jeito de relacionar a posição da barra com o ângulo .
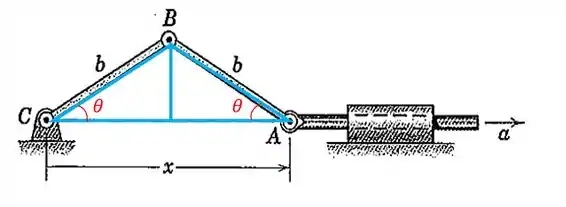
Para isso, repare nos dois triângulos retângulos que as barras formam:
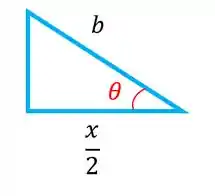
Usando trigonometria obtemos a seguinte relação:
Então:
Pronto, temos a equação da posição da barra .
Passo 2
Vamos derivar a equação da posição para obtermos a velocidade:
O comprimento das barras é constante e o ângulo depende do tempo, então vamos aplicar a regra da cadeia:
Não esqueça que a velocidade angular é:
Então, vamos ter:
A questão pede a velocidade angular da barra , então vamos isolar ela na equação:
Passo 3
Repare que a questão pede a velocidade angular da barra em função de e da aceleração . Veja que o enunciado disse que a aceleração é constante, então podemos usar uma daquelas equações de movimento retilíneo para aceleração constante.
Mas tem que ser uma equação que relacione a velocidade, a aceleração e a posição. Vamos usar essa aqui:
Sabemos que as barrinhas partem do repouso e que a velocidade inicial é nula, então:
Então:
Opa, agora vamos substituir isso na equação da velocidade angular :
Agora só falta retirarmos a variável da equação e fazer aparecer o . Nesta parte vamos ter aquela sacada de mestre. Sabemos da trigonometria que:
Isolando o vamos ter:
Vamos substituir isso na nossa equação:
Por que fizemos isso? Porque a equação que aparece o é a primeira que achamos:
E nessa equação também aparece o , por isso tínhamos que fazer aparecer o na nossa equação de velocidade angular.

Está quase terminando...
Vamos isolar o :
E agora substituir na equação da velocidade angular:
Pronto? Teoricamente sim, mas podemos deixar nossa equação mais bonitinha. Para isso, vamos passar o para dentro da raiz:
E é só alegria:
Esse sinal negativo indica que a velocidade angular está no sentido horário, então podemos escrever:
Resposta
Exercício Resolvido #4
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 252-5/31
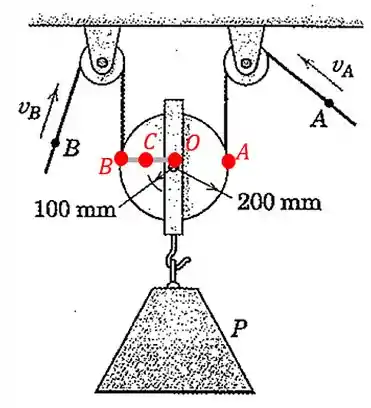
O bloco de concreto está sendo abaixado pelo arranjo de cabo e polia mostrado. Se os pontos e têm velocidades de e , respectivamente, calcule a velocidade de , a velocidade do ponto para o instante representado, e a velocidade angular da polia.
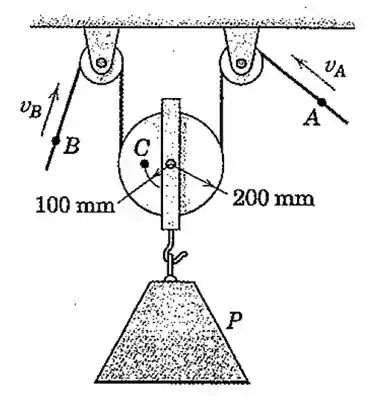
Passo 1
A velocidade do ponto é igual a velocidade onde o cabo do lado esquerdo encontra a polia central. E a mesma coisa ocorre no ponto onde o cabo do lado direito encontra a polia do meio. Então, vou chamar esses pontos também de e por terem a mesma velocidade:
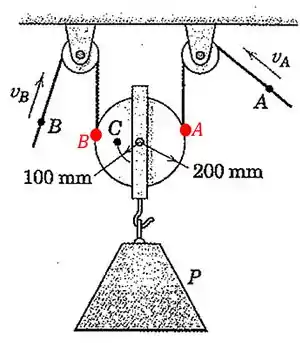
Vamos fazer uma linha ligando os pontos , e para ver o que está acontecendo:
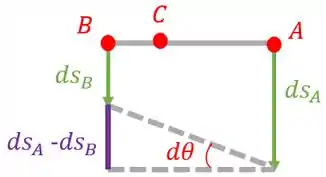
Repare que os vetores e apontam para baixo, porque o bloco está descendo. E como a velocidade do ponto é maior do que a velocidade do ponto , vamos ter que:
Passo 2
Agora vamos analisar como um movimento circular:
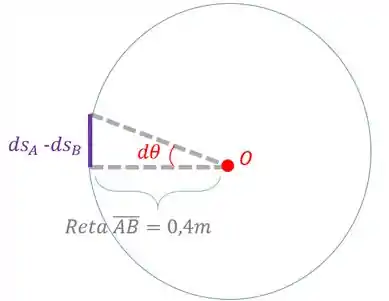
Vamos ter que a variação da posição entre os pontos e () será igual ao comprimento do arco do círculo que é a trajetória do movimento:
Agora é só derivar para achar a velocidade:
Sabendo que:
Então:
Vamos isolar a velocidade angular que é o que não sabemos:
Vamos substituir o que já sabemos: , e
Essa é a velocidade angular da polia.
Passo 3
Agora temos que achar a velocidade do bloco . Para isso, vamos fazer uma reta ligando os pontos e o centro da polia que vamos chamar de :
Teremos o seguinte:
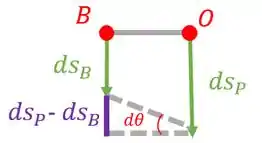
A nossa equação da posição vai ficar:
Para achar a velocidade é só derivar:
Como queremos a velocidade do bloquinho , então vamos isolar na equação:
Já sabemos que , e , então:
Passo 4
Agora falta acharmos a velocidade do ponto . Para isso, vamos fazer uma reta ligando os pontos e :
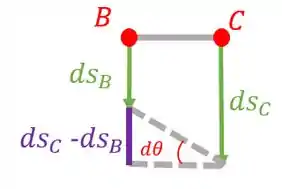
Temos que:
Para saber a velocidade do ponto é só derivar:
Vamos isolar que é o que queremos saber:
Repare que é:
Agora é só substituirmos os valores que já temos: ,
Essa é a velocidade do ponto .
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 260-16.39
No instante em que , a guia está subindo com aceleração de e velocidade de . Determine a aceleração e a velocidade angulares da barra no instante em considerado. Observação: o movimento para cima da guia ocorre no sentido negativo de .
Dado:
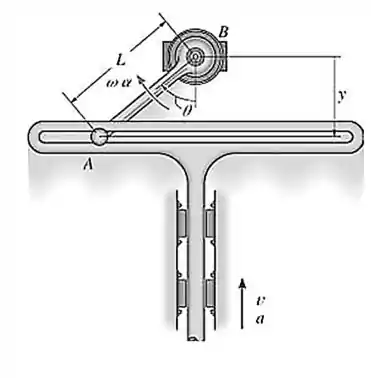
Passo 1
O que temos que fazer nesses tipos de questões é achar uma relação trigonométrica entre o que queremos saber e o que temos de informação.
Para começar vamos colocar em função das nossas informações:
Podemos dizer que:
Derivando isso, vamos achar a equação da velocidade. Para derivar isso aí temos que usar a regra da cadeia:
Com essa equação podemos achar a velocidade angular da barra , pois sabemos que e .
Repare que o sentido positivo do eixo é apontando para baixo, certo? Então, a velocidade será negativa:
Agora vamos substituir tudo na nossa equação:
Passo 2
Derivando agora a equação da velocidade, vamos obter a equação da aceleração. Mas para derivar temos que usar a regra da cadeia e a regra do produto:
Com essa equação vamos achar a aceleração angular da barra .
Mas antes repare que a aceleração da guia está apontando no sentido negativo do eixo , então:
Substituindo o que temos:
Resposta
Exercício Resolvido #6
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 256-5/53
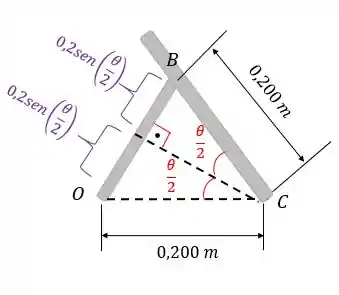
O acionamento do cilindro hidráulico provoca o alongamento de na taxa constante de . Calcule a aceleração normal do ponto em sua trajetória circular em torno de para o instante em que .
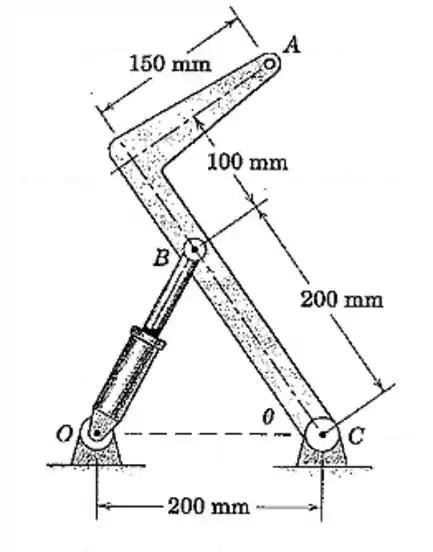
Passo 1
Nesses tipos de questões temos que achar uma relação trigonométrica entre o que queremos saber e o que temos de informação. A informação que temos é que a velocidade de é de . Então, vamos achar alguma relação trigonométrica com o comprimento :
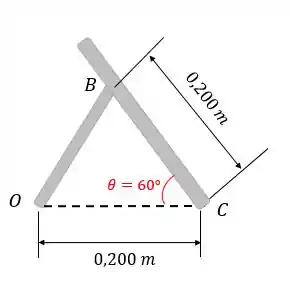
Repare neste triângulo formado. Podemos escrever o comprimento como:
Passo 2
Derivando a equação que achamos vamos obter a equação da velocidade:
Para resolver esta derivada temos que usar a regra da cadeia, pois o ângulo varia no tempo:
Como e a velocidade de é , então:
Essa é a velocidade angular com que gira em torno de .
Passo 3
Agora vamos ver o que está acontecendo com o ponto :
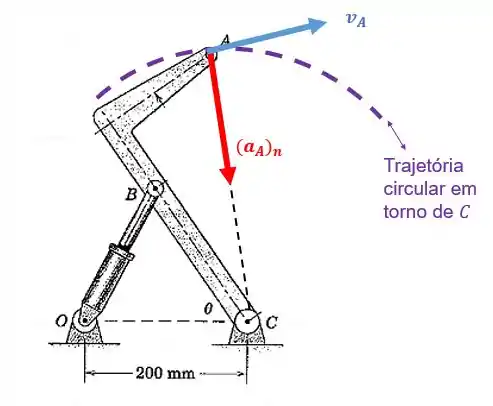
A questão pede a aceleração normal que é calculada pela seguinte fórmula:
Para achar o raio, vamos usar o seguinte triângulo:
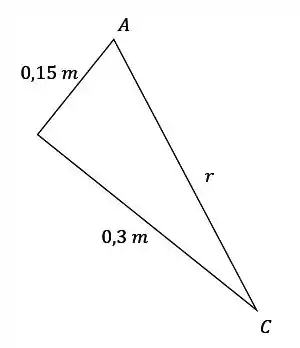
Como é um triângulo retângulo, vamos aplicar o Teorema de Pitágoras:
Agora sim podemos calcular a aceleração normal do ponto :
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 261-16.45
A barra gira uniformemente em torno do pino , com velocidade angular constante . Determine a velocidade e a aceleração do bloco , no instante em que .
Dados: ; .
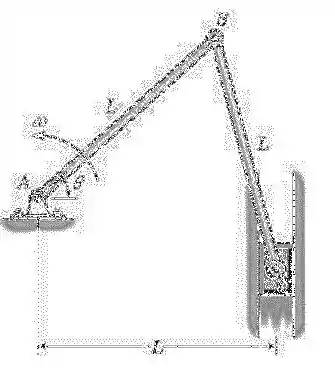
Passo 1
O que temos que fazer nesses tipos de questões é achar uma relação trigonométrica entre o que queremos saber e o que temos de informação. A questão quer saber o movimento de quando :
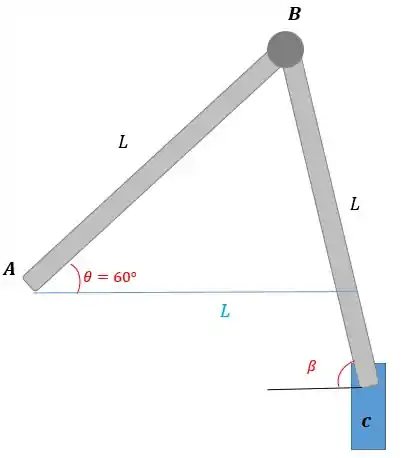
Temos que o comprimento da base pode ser escrito como:
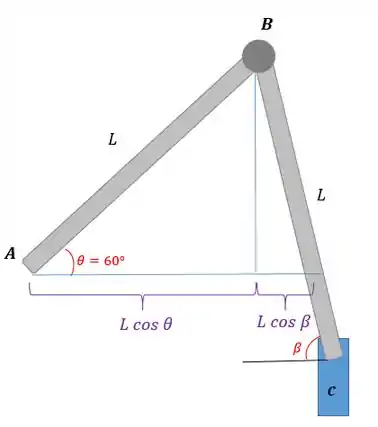
Dividindo toda nossa equação por , temos:
Sabemos que , então:
Passo 2
Nós temos a seguinte relação:
Agora vamos derivar isso, para relacionar as velocidades angulares de e :
Sabemos que:
Como e , então:
Passo 3
Vamos derivar a equação que achamos no passo anterior para acharmos uma relação entre as acelerações angulares:
Para derivar isso temos que usar a regra da cadeia e a regra do produto e vamos ficar com:
Repare que a velocidade angular da barra é constante, então a sua velocidade angular será zero:
Vamos substituir o que temos:
Passo 4
Agora vamos achar uma equação que relacione o deslocamento vertical do bloco :
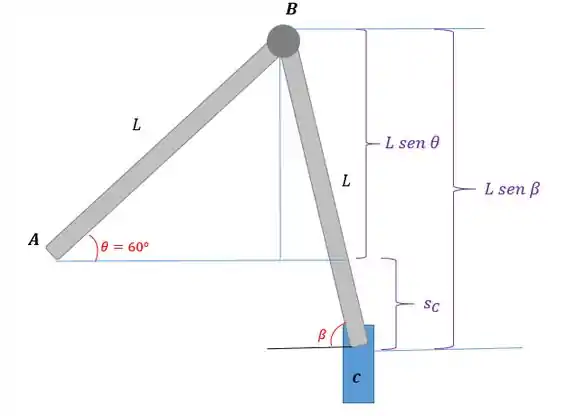
Repare que o deslocamento vertical do ponto será:
Sabemos que , e , então:
Ou seja, não teve deslocamento vertical.
Passo 5
Agora vamos derivar essa equação que achamos para achar uma equação para a velocidade de :
Substituindo o que temos:
Passo 6
Para acharmos a aceleração do bloco , temos que derivar a equação da velocidade que acabamos de encontrar:
Vamos ter que:
Substituindo os valores que já temos: