Movimento Relativo: Velocidade
Teoria
Introdução
Se tivermos duas barrinhas articulas entre si:
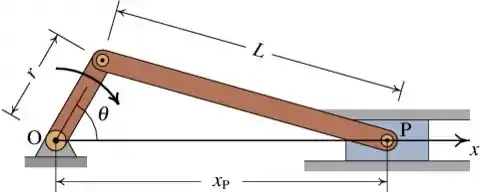
Se quisermos saber a velocidade que o ponto tem em relação ao ponto vamos ter que trabalhar de um jeito diferente com o conceito de velocidade relativa.
Neste capítulo vamos aprender a achar a velocidade relativa entre pontos que pertencem a um mesmo corpo rígido. Partiu?
- Velocidade Relativa
Quando você tem um corpo rígido realizando rotação e translação ao mesmo tempo, e você quer saber a velocidade que um ponto deste corpo possui com relação a um ponto que também pertence a esse mesmo corpo, vamos usar a seguinte equação:
A velocidade relativa de com relação a nós chamamos de . Ela é a velocidade que um observador que está no ponto vê o ponto se movendo.
Mas o ponto que o observador está (ponto ) sofre os mesmo movimentos de translação que o ponto que ele está observando:
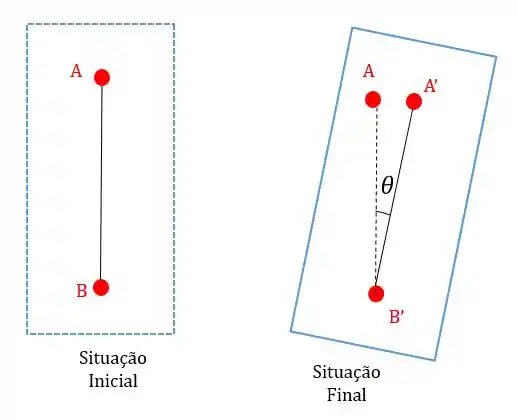
Ou seja, para um observador no ponto é como se o ponto estivesse girando em torno dele:
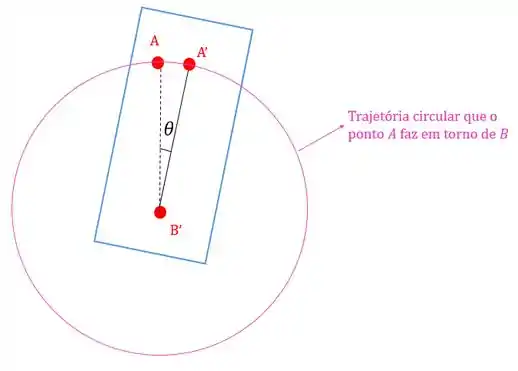
Repare que o raio desta trajetória é a distância entre os ponto e . Então, a velocidade relativa de com relação a será calculada usando a equação da rotação:
Onde, é a velocidade angular do corpo que os pontos e pertencem. O vetor velocidade angular está sempre no eixo e o seu sentido será dado pela regra da mão direita:
Já o vetor é o raio da trajetória circular que o ponto que está sendo observado faz em torno do ponto em que está o observador:
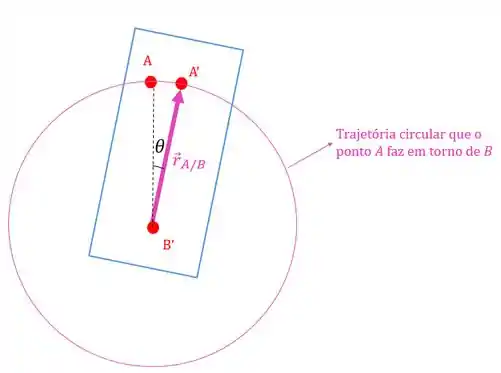
E como sabemos onde o vetor começa e onde termina?
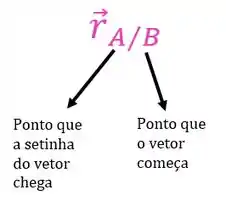
E uma coisa importante: Como se faz produto vetorial mesmo?
Vamos supor que temos os seguintes vetores:
E:
E queremos fazer o produto vetorial entre eles:
Isso vai ser igual a:
Para resolver isso temos que montar a seguinte matriz:
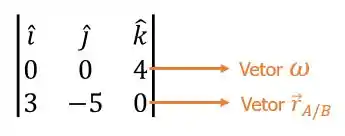
Agora vamos separar em matrizes para facilitar nossa vida. Para achar a componente é só cortar a linha e a coluna onde está o e achar o determinante da matriz que sobrou:
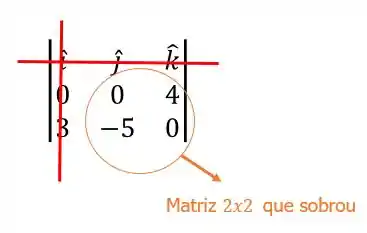
A componente será:
Para as outras componentes é só fazer a mesma coisa e não esquecer de multiplicar por o resultado da componente :
Beleza?
Agora vamos resolver aquele exemplo para entendermos melhor!
Se quisermos só o módulo da velocidade relativa de com relação a é só fazermos:
O vetor velocidade relativa () vai ser sempre perpendicular ao vetor que une os pontos e (:
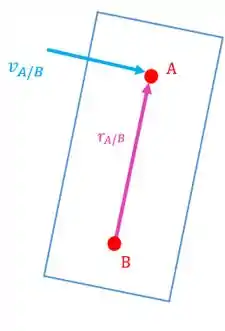
Vamos praticar para pegar o jeito!!! 
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 264-5/70
O disco circular rola sem deslizar com uma velocidade angular no sentido horário . Para o instante representado, escreva as expressões vetoriais para a velocidade de com relação a e para a velocidade de .
Passo 1
Primeiro, vamos achar a velocidade de com relação a :
A velocidade angular está sempre no eixo . Mas qual é o seu sinal? Repare que a velocidade angular faz o disco girar no sentido horário e este sentido foi o que estabelecemos como negativo:
Repare também que a velocidade angular é a mesma para todos os pontos que pertencem ao disco:
Beleza?
Falta acharmos o valor de :
Não se esqueça que o vetor vai ter sua origem no ponto e vai chegar no ponto , já que o exercício quer a velocidade de com relação a . 
Como vamos fazer um produto vetorial, vamos decompor o vetor :
Agora é só substituirmos:
Vamos montar nossa matriz para fazer o produto vetorial:
Então, a velocidade de com relação a :
Passo 2
Agora vamos achar a velocidade do ponto . Repare que o ponto gira em torno do ponto que é o centro do círculo:
Vamos ter que:
Onde:
Vamos fazer esse produto vetorial. Sabendo que:
Então:
E a velocidade do ponto ()? Como o círculo anda para a direita, então o sentido da velocidade do ponto é:
Agora é só usarmos a fórmula da rotação para achar o seu módulo:
Então, a velocidade do ponto será:
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 272-16.68
Se a extremidade da corda está sendo puxada com velocidade , determine as velocidades angulares das polias e e a velocidade do bloco . Suponha que a corda não escorregue nas polias.
Passo 1
Vamos analisar a polia primeiro. Repare que esta polia está presa, ou seja, ela só pode girar em torno do seu e centro. Então, vamos usar a equação do movimento de rotação:
Qual é a velocidade que a polia () possui? Nesses problemas admitimos que as cordas são inextensíveis, ou seja, elas não variam de comprimento nem nada. Então, a velocidade por toda a corda é a mesma:
Então, podemos escrever que:
O que queremos saber é a velocidade angular da polia , então:
Vamos ter:
Repare que não precisa pssar o raio para metros, porque a velocidade foi dada em !!!
Passo 2
Agora vamos analisar a polia . Repare que esta polia não está presa, então ele sofre rotação e deslocamento. Quando temos uma polia nesta situação, temos que usar o nosso esquema:
Mas sabemos que a velocidade por toda a corda é a mesma, então:
Podemos reescrever nossa equação assim:
Pronto, agora é só substituir os valores:
Passo 3
Está faltando acharmos a velocidade com que o bloco sobe:
Para achar vamos usar os dado que temos do movimento da polia :
Resposta
Exercício Resolvido #3
J.L. Meriam e L.G. Kraige,Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 265-5/73
A unidade consiste em um motor com redução de alto torque que gira a barra na taxa constante . A unidade é livre para se mover ao longo da superfície horizontal. Determine a velocidade da unidade quando atinge .
Passo 1
Vamos entender o que está acontecendo... Conforme o ângulo aumenta, o ponto se move para a direta.
Então, vamos ter que:
Vamos achar o vetor primeiro, lembrando que:
Para isso, temos que decompor :
E o vetor fica sempre no eixo Falta saber se ele é positivo ou negativo. Mas é só olhar como ele faz a barra girar, que no nosso caso é no sentido anti-horário, ou seja, é positivo:
Pronto! Podemos fazer o produto vetorial:
Então:
Seu módulo será:
O vetor fica assim:
Passo 2
Vamos agora analisar o vetor . Repare também que o ponto tende a girar em torno do ponto fixo , de modo que a velocidade neste ponto é tangente à trajetória circular
Repare que para achar a velocidade do ponto , teríamos que achar a velocidade relativa da barra :
Isso daria muito trabalho... Então, vamos usar a lei dos senos:
Mas antes temos que achar esses ângulos entre os vetores. Vamos começar pelo ângulo que o vetor faz com a horizontal:
Repare que o ângulo que o vetor faz com a horizontal vai ser:
Podemos achar quanto vale o ângulo pela geometria inicial do nosso problema e utilizando a lei dos senos também:
Então, este ângulo vai ser:
Podemos achar o valor de :
Agora vamos achar o ângulo que o vetor faz com relação a horizontal:
Então, já temos até agora:
O ângulo será:
Agora podemos aplicar a lei dos senos para achar o valor de :
O vetor aponta no sentido positivo do eixo , então podemos escrever o vetor como:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 270-16.54
O mecanismo mostrado na figura foi desenvolvido para dar à lâmina presa no cursor um golpe lento e retornar rapidamente. Determine a velocidade do cursor no instante em que , se a barra gira a .
Passo 1
Primeiro vamos entender o que está acontecendo. A barra está girando em torno do ponto fazendo com que a barra se mova. O que queremos saber é a velocidade no ponto . Então, o nosso diagrama cinemático fica assim:
Calma, vamos analisar cada barra separadamente. Mas qual devemos analisar primeiro? A barra que tenha sido dada alguma informação sobre ela na questão. No nosso caso é a barra . Repare que o ponto realiza um movimento circular em torno do ponto :
Repare que o vetor velocidade é tangente à trajetória. Como o movimento de é somente de rotação em torno de , vamos usar a equação do movimento de rotação:
Passo 2
Precisamos fazer o produto vetorial, então vamos decompor o vetor em relação ao eixo :
Sabemos que a velocidade angular tem apenas uma componente no eixo só falta sabermos se ela aponta para o sentido positivo ou negativo deste eixo. Lembra que definimos que quando a velocidade angular gira no sentido anti-horário ela é positiva? Como está girando neste sentido, ela é positiva:
Nosso produto vetorial vai ficar assim:
Para resolver o produto vetorial é só lembrar que para cada componente é só excluir a linha e a coluna correspondente. Se for por exemplo a componente no eixo :
Agora é só acharmos os determinantes dessas matrizes :
Então, a velocidade no ponto será:
Passo 3
Agora vamos fazer nossa análise para a barra :
Vamos ter que:
Sendo que a velocidade relativa do ponto com relação ao ponto () é:
Vamos decompor o raio :
A aceleração angular da barra também gira no sentido anti-horário, ou seja, ela é positiva:
Então, vamos ter o seguinte produto vetorial:
Que pode ser escrito assim:
A velocidade será:
Passo 4
Agora que sabemos a velocidade relativa de com relação a e o valor de vamos substituir na equação para achar :
Teremos:
Mas repare que o cursor só pode se mover na horizontal, de modo que a sua velocidade será:
Então, podemos escrever:
Agora é só somarmos todos os termos de mesma componente ( com e com ) . Vamos ter o seguinte sistema:
E:
De cara podemos achar o valor de pela segunda equação:
Substituindo isso na primeira equação:
O vetor velocidade do ponto vai ser:
Como o sinal deu negativo, significa que a velocidade aponta no sentido negativo do eixo .
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 270-16.56
A velocidade do cursor C é de 4 pés/s tubo acima. Determine a velocidade angular das barras AB e BC e a velocidade do ponto B na situação mostrada na figura.
Passo 1
Vamos começar montando a equação da velocidade do ponto :
Vamos adotar esses vetores da figura, caso estejam no sentido errado, o resultado vai dar negativo.
O vetor posição será:
E como o nosso sistema de referência adota o sentido anti-horário como positivo, o vetor velocidade angular será negativo, pois faz a barra girar no sentido horário:
Então, nossa equação fica:
O produto vetorial vai ficar assim:
Passo 2
Agora vamos para a barra . Temos que:
Vamos considerar os vetores como está na figura. Então:
E a velocidade angular da barra é positiva, pois está girando no sentido anti-horário:
Agora vamos decompor o vetor :
Como , temos que:
Beleza?
Agora podemos substituir o que temos na nossa equação da barra :
Vamos resolver o produto vetorial:
Então:
Vamos igualar os termos de mesma componente:
Como deu tudo positivo, significa que escolhemos o sentido correto dos vetores, então a velocidade angular das barras é:
Passo 3
Agora podemos calcular a velocidade do ponto :
E seu módulo é:
Resposta
Exercício Resolvido #6
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 266-5/81
A extremidade da barra possui uma velocidade para baixo de durante um intervalo de seu movimento. Para a posição em que determine a velocidade angular de e a velocidade do ponto central da barra. Resolva as equações da velocidade relativa, inicialmente utilizando geometria do polígono de vetores e, em seguida, utilizando a álgebra vetorial.
Passo 1
Quando a extremidade se move para baixo, a extremidade da mesma barra se move para a esquerda:
Sabemos que a velocidade angular é calculada da seguinte forma:
Então, a velocidade angular da barra será:
Mas como calcular a velocidade de com relação a ? Para achar seu valor vamos ter que fazer uma soma dos vetores velocidade que temos. Mas lembre-se que a velocidade relativa é sempre perpendicular à linha que une os dois pontos, ou seja, no nosso caso o vetor vai ser perpendicular a barra :
O triângulo de velocidades fica assim:
Agora vamos achar os ângulos entre os vetores:
Para achar o ângulo temos que fazer a seguinte sequência:
Então, será:
A velocidade do ponto nós temos e vale , então:
Com esse valor podemos calcular a velocidade angular da barra :
Para determinar o sinal da velocidade angular usamos a regra da mão direita: temos que colocar os quatro dedos da palma da mão direita no sentido do vetor e com isso o seu dedão vai apontar para o sentido positivo do eixo (para dentro da tela). Ou seja, a velocidade angular faz a barra girar no sentido horário:
O sentido horário é positivo devido a posição do eixo !!!
Passo 2
Agora temos que calcular a mesma coisa do passo anterior, porém de forma vetorial. Para isso, vamos usar a equação da velocidade relativa. Temos que a velocidade da extremidade é:
O vetor posição de em relação a quando é:
Sabemos que o vetor é:
O vetor aponta no sentido positivo do eixo e podemos calcular o seu valor através do triângulo de velocidades:
Então, o vetor é:
Como estamos fazendo de conta que não sabemos o valor da velocidade angular, podemos dizer apenas que:
Depois vamos descobrir se é positivo mesmo ou negativo.
Passo 3
Vamos substituir o que temos na equação da velocidade:
Nosso produto vetorial vai ficar:
Então:
Somando os termos da mesma componente:
O valor de é:
Como encontrado antes!!!
Passo 4
Agora vamos achar o valor da velocidade do ponto central da barra utilizando o triângulo de velocidades.
Sabemos que o vetor velocidade relativa de com relação a é perpendicular à reta que liga os pontos e :
Então, o triângulo de velocidades vai ficar:
Temos o mesmo ângulo entre os vetores:
Repare que podemos calcular , pois já sabemos a velocidade angular da barra:
Agora para saber o valor de é só usarmos a lei dos cossenos:
Passo 5
Agora vamos calcular a velocidade utilizando a equação da velocidade:
O vetor posição será:
Então, o vetor vai ser:
E seu módulo é:
Resposta
Exercício Resolvido #7
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 267-5/88
No mecanismo de três barras mostrado, a haste de controle possui uma velocidade angular no sentido anti-horário durante um curto intervalo de movimento. Quando a haste ultrapassa a posição vertical mostrada, o ponto possui as coordenadas e . Determine por meio da álgebra vetorial as velocidades angulares de e .
Passo 1
Vamos começar pela barra , pois sabemos a sua velocidade angular. Repare que o ponto gira em torno do ponto , então podemos escrever:
Sabemos que a velocidade angular da barra é no sentido anti-horário, então ela é positiva:
E o vetor posição ?
Ao decompor o vetor , temos:
Repare que a origem do eixo está em cima do ponto !!!
Então, vamos ter que:
Esse produto vetorial fica assim:
Então:
Passo 2
Agora vamos analisar a barra . Repare que o ponto gira em torno do ponto , então:
Nós não sabemos a velocidade angular da barra , então vamos arbitrar o sentido positivo:
E a posição é:
Vamos ter que:
Fazendo o produto vetorial vamos ter:
Passo 3
Agora vamos analisar a barra :
A velocidade angular da barra nós não sabemos, mas vamos arbitrar o sentido como positivo (anti-horário):
A posição é:
Agora vamos substituir o já temos:
O produto vetorial fica:
Então:
Agora vamos somar os termos da mesma componente:
Da equação em temos que:
Como achamos um valor positivo, significa que arbitramos o sentido certo para :
Agora vamos usar a equação das componentes em :
Como achamos um valor positivo, significa que arbitramos o sentido correto para :