Movimento Curvilíneo e Forças
Produzido por Pablo RicardoTeoria
Introdução
Sabe por que o trem da montanha-russa não cai?

Porque existe uma força que atua no corpo sempre que ele realiza um movimento circular e ela é responsável por não deixar o corpo sair dessa trajetória curvilínea. E qual o nome desta força mágica? É a força centrípeta....
Esta força é responsável por gerar uma mudança na direção do vetor velocidade , mas sem alterar o seu módulo. Vamos estudar a força centrípeta e a sua causa neste capítulo.
Movimento Curvilíneo
Sempre que um corpo realiza um movimento circular, o vetor velocidade vai mudando de sentido e direção. Imagine um motoqueiro percorrendo o globo da morte:
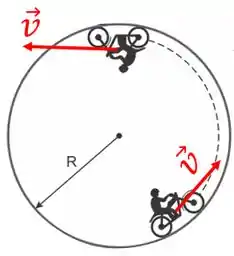
O globo da morte é uma esfera oca onde o motociclista fica andando em seu interior. Repare que o vetor velocidade é sempre tangente ao círculo e tem módulo constante. A grandeza responsável pela mudança da direção e do sentido do vetor velocidade fazendo ele seguir uma trajetória circular é a aceleração centrípeta:
Esse é o raio da curvatura realizada. Se for um círculo, é o raio do círculo mesmo.
A aceleração centrípeta é uma grandeza vetorial e sempre aponta para o centro da trajetória circular. (Colocamos o vetorzinho só para você se lembrar disso que acabamos de dizer ![]() )
)
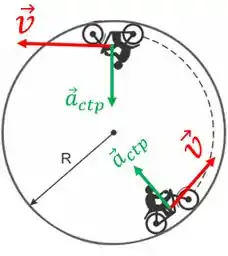
Entãããooo...Se quisermos calcular o módulo da força centrípeta:
E caso tenhamos a velocidade angular , a aceleração centrípeta vai ser:
Onde tem uma aceleração também tem uma força resultante, certo? É só lembrar da segunda lei de Newton: .
Então...
Força Centrípeta
Quando o movimento é circular, a força resultante que aponta para dentro do círculo recebe um nome especial: força centrípeta . E como fazemos para calcular? É só lembrar da segunda lei de Newton e trocar para as grandezas que são características do movimento circular:
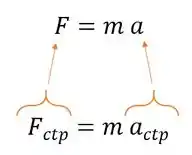
Então:
Lembre que a força centrípeta vai apontar para o centro da trajetória circular.
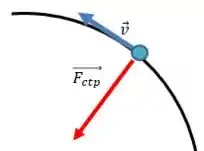
Não podemos esquecer que a velocidade angular se relaciona com a velocidade tangencial assim:
Se substituirmos isso na equação da força centrípeta obtemos:
Vamos guardar essas fórmulas de força centrípeta! ![]()
Para resolvermos os exercícios, temos que seguir o seguinte passo a passo:
- Isolar o corpo principal do problema e colocar TODAS as forças que estão atuando nele.
- Achar a resultante de forças que apontam para o centro da trajetória circular e aplicar a segunda lei de Newton para a movimento curvilíneo.
Vamos resolver um exemplo para ficar mais claro...
Imagina o nosso motoqueiro andando no globo da morte. Qual seria a menor velocidade que ele precisa ter para não cair ao passar no ponto mais alto do globo?
Primeiro passo: colocar todas as forças que atuam no motoqueiro quando ele estiver no ponto mais alto:
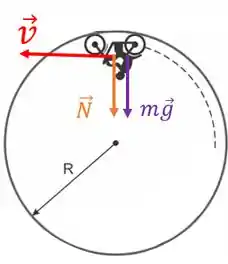
Observe que a força normal surge devido ao contato da moto com a superfície do globo. Mas para sabermos a velocidade mínima que o motoqueiro precisa ter para não cair, temos que considerar a pior situação de todas.
A pior situação ocorre justamente quando ele está na iminência de cair. Quando o contato entre a moto e a superfície do globo é tão pequena que podemos considerar nula.
Segundo passo: a força resultante na direção do centro do círculo é a força centrípeta:
Terceiro passo: aplicar a segunda lei de Newton para a movimento curvilíneo:
Portanto, a velocidade mínima será:
Repare que ela não depende da massa, apenas da gravidade e do raio do círculo!!!
Vamos praticar mais isso aí!!! ![]()
Força Centrípeta
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 104, 3/49
O pequeno bloco de desliza para baixo na trajetória curva e passa pelo ponto mais baixo com uma velocidade de . Se o raio de curvatura da trajetória em é de , determine a força normal exercida sobre o bloco pela trajetória neste ponto. É necessário o conhecimento das propriedades de atrito?
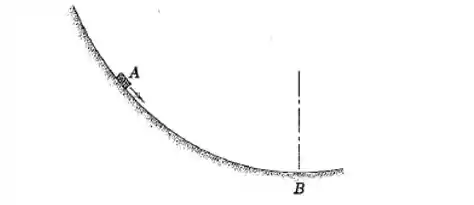
Passo 1
O sistema do problema no ponto pode se representado por:
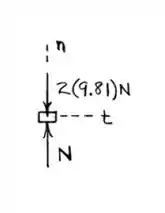
Como o corpo está realizando um movimento curvilíneo:
Assim:
Passo 2
E ai? O atrito entrou na conta?
Não né?
Bom, a força de atrito é perpendicular à força Normal. Assim, ela não vai influenciar a mesma.
Então, a resposta é Não.
Resposta
Não
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 106, 3/60
Uma criança gira uma pequena esfera de presa na extremidade de um fio com de modo que a esfera traça um círculo em um plano vertical como mostrado. Qual é a velocidade mínima que a esfera deve ter quando estiver na posição 1? Se essa velocidade é mantida ao longo do círculo, calcule a tração no fio quando a esfera está na posição 2. Despreze qualquer pequeno movimento da mão da criança.
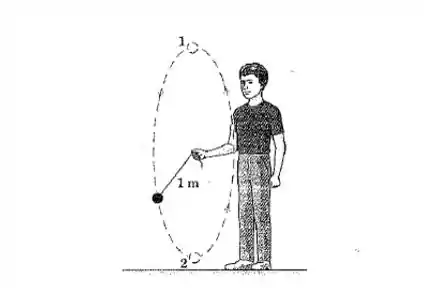
Passo 1
Pro caso da velocidade mínima, devemos ter Assim:
Assim:
Passo 2
Basta agora a gente aplicar:
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 104, 3/51
Se o bloco de passa sobre o topo da porção circular da trajetória com velocidade de , calcule o módulo da força normal exercida pela trajetória sobre o bloco. Determine a velocidade máxima que o bloco pode ter em sem que perca o contato com a trajetória.
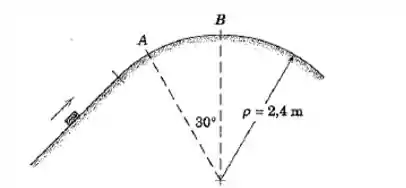
Passo 1
Vamos calcular primeiro para o caso do enunciado:
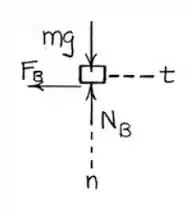
Assim, temos:
Passo 2
No outro caso:
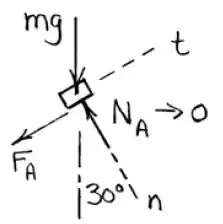
Como estamos estimando a velocidade para que o corpo perca o contato, devemos considerar que
Agora, precisamos apenas decompor a força peso na direção radial e comparar com a resultante:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 105, 3/54
Determine o ângulo de inclinação lateral apropriado para o avião voando a e execuando um curva com de raio. Note que a força exercida pelo ar é normal à superfície de apoio da asa. Dado:
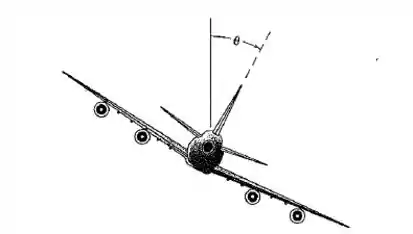
Passo 1
O avião pode ser esquematizado por:
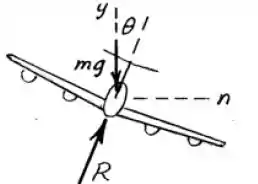
O equilíbrio em será dado por:
Passo 2
Horizontalmente, teremos a resultante centrípeta igual a
Dividindo uma equação por outra:
Assim:
Vamos converter a velocidade e pra
E:
Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 108, 3/73
Uma pequena conta de massa é conduzida por um aro circular de raio que gira em torno de um eixo vertical fixo. Mostre como se pode determinar a velocidade angular do aro pela observaçaõ do ângulo que localiza a conta. Despreze o atrito em sua análise , mas assuma que uma pequena quantidade de atrito está presente para amortecer qualquer movimento da conta em relação ao aro uma vez que uma velocidade angular constante tenha sido estabelecida. Aponte quaisquer restrições sobre sua solução.
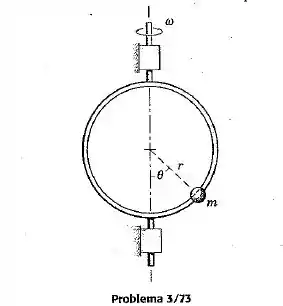
Passo 1
Vamos lá: Pelo enunciado sabemos que, ao atingir certa velocidade angular, a conta ficará numa posição “angular” fixa: aquele ângulo não vai mudar.
As forças que agem na conta são a força Normal e o Peso:
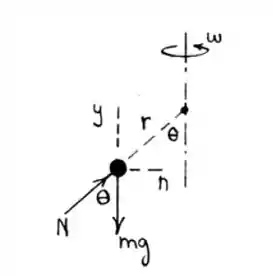
Pelo o equilíbrio vertical, temos:
Passo 2
Horizontalmente falando, temos uma resultante que é centrípeta. Assim:
Ai vem um pulo do gato. Lembra que Então:
Substituindo o valor de
Mas quem é , o raio de giração? Não é exatamente a , o raio do círculo, já que existe uma certa inclinação. Sendo assim:
Agora:
Pronto (:
Passo 3
Vamos pensar nas restrições agora: Veja que na solução existe um cosseno. Senos e cossenos sempre possuem uma restrição que é:
Assim:
Aplicando a restrição:
Resposta
Com
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 108, 3/67
Um piloto voa em um avião a uma velocidade constante de no círculo vertical com um raio de . Calcule a força exercida pelo assento spbre o piloto de no ponto e no ponto .
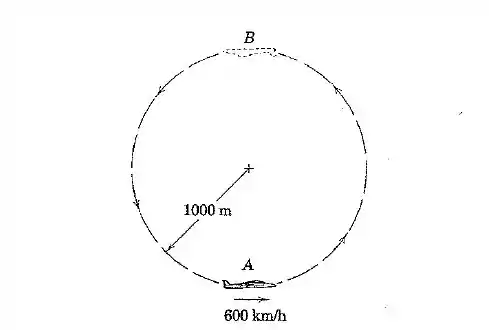
Passo 1
Bom, o avião está dando um loop. Meio bizarro isso né? Mas vamos lá:
No ponto A:
A resultante das forças é centrípeta, então aponta para o centro. Por outro lado, a força do assento é sempre norma ao assento, sendo assim, nesse caso, aponta para cima:
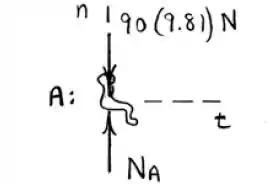
Primeiro vamos converter a velocidade para :
Assim:
Passo 2
Ponto B:
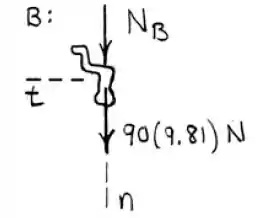
Da mesma forma:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 108, 3/74
O cursor de se encaixa com folga na ranhura lisa de no disco, que gira em um plano horizontal em torno do seu centro . Se é mantido em posição por um cordão fixo no ponto , determine a tração no cordão para uma velocidade rotacional constante . A direção da velocidade faria alguma diferença?
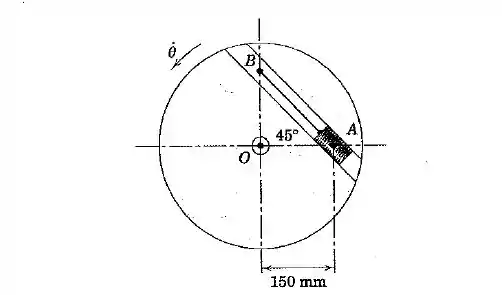
Passo 1
Vamos representar o sistema por:
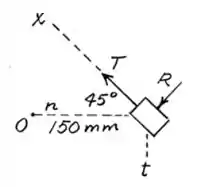
Sendo a componente centrípeta uma componente da força , o que nos dá:
Onde é a força centrípeta.
A força centrípeta estará apontando na direção normal. Podemos calcular a aceleração nessa direção assim:
A conversão de para é:
Assim:
Passo 2
Assim, para achar , vamos calcular o equilíbrio de forças na direção