Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 59
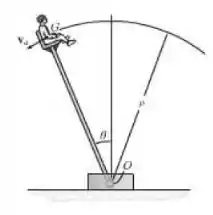
Um acrobata tem peso de 750 N e está sentado em uma cadeira que está fixada no topo de um mastro, como mostrado. Se por um acionamento mecânico o mastro gira para baixo com uma razão constante a partir de de tal maneira que o centro de massa G do acrobata mantenha uma velocidade constante , determine o ângulo no qual ele começa a “voar” para fora da cadeira. Despreze o atrito e suponha que a distância do axial O a G é .
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Passo 2
Vamos começar por esboçar o diagrama de corpo livre. Considerando a pessoa como uma partícula o seguinte diagrama:
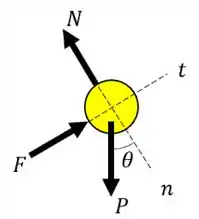
A pessoa está sujeita a duas reações da cadeira, uma na direção tangencial, a qual está relacionada ao apoio das costas da cadeira, e outra na direção da força normal, a qual é devido ao assento. Está na direção normal é a força normal.
Como a pessoa está na iminência de “voar”, significa que a força normal é nula!
Passo 3
Para descobrirmos o ângulo que faz com que a pessoa fique na iminência de “voar”, basta considerarmos a força normal nula e fazermos o somatório de forças na direção normal. Portanto,