Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 55
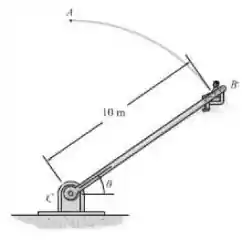
O dispositivo mostrado é usado para produzir a experiência de gravidade zero em um passageiro quando ele atinge o ponto A, , ao longo da trajetória. Se o passageiro tem massa de 75 kg, determine a velocidade mínima que ele deve ter quando alcança A de maneira que ele não exerça uma reação normal sobre o assento. A cadeira é presa por um pino à estrutura BC de maneira que ele está sempre sentado em uma posição vertical. Durante o movimento sua velocidade permanece constante.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Vamos a questão então!
Passo 2
Vamos começar por esboçar o diagrama de corpo livre. Considerando a pessoa como uma partícula, para , temos o seguinte diagrama:
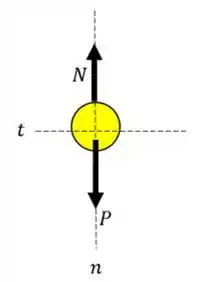
Como a pessoa não exerce nenhuma reação normal, ele está sujeito apenas a força peso!
Passo 3
Para descobrirmos a velocidade mínima da pessoa, basta fazermos o somatório das forças na direção normal. Portanto,