Determine o coeficiente de atrito estático entre os pneus e a superfície da estrada é , determine a velocidade máxima do carro de 1,5 Mg de modo que ele não deslize quando ele se move na curva. Despreze a dimensão do carro.

Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:
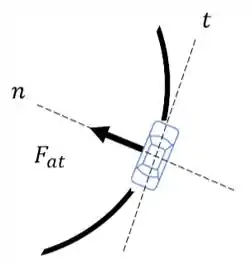
Portanto, o carro está sujeito apenas a ação da força de atrito na direção normal a curva!
Passo 3
Antes de começarmos a nossa análise, vamos escrever quem é a força de atrito. Portanto, temos:
Fazendo o somatório das forças na direção normal, temos:
Portanto,