Movimento Relativo: Aceleração
Produzido por Pablo RicardoTeoria
Introdução
Agora que vimos como achar a velocidade relativa entre diversos pontos que pertencem a um corpo rígido, vamos trabalhar com a aceleração.
Lembra das nossas barrinhas articuladas?
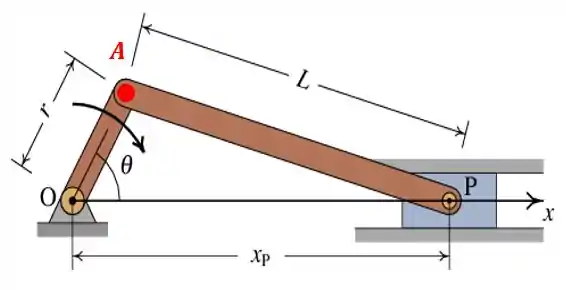
E se ao invés da velocidade eu queira saber a aceleração relativa entre os ponto e ? É isso que vamos ver neste capítulo, como relacionar as acelerações de pontos diferentes que pertencem ao mesmo corpo rígido.
Você vai ver que é bem parecido com o que vimos para a velocidade. Vamos começar!
- Aceleração Relativa
Para chegamos na equação que relaciona a aceleração de dois pontos e de um mesmo corpo rígido com a aceleração relativa entre esses pontos é só derivarmos a equação da velocidade:
Vamos ter que:
Lembra que para um observador em o ponto realiza um movimento circular?
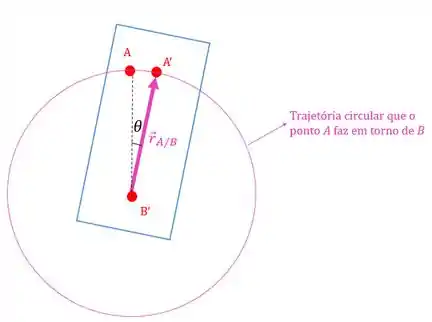
Como o movimento é circular, a aceleração relativa vai ter uma componente tangencial e outra componente normal :
Para calcular a componente tangencial da aceleração usamos:
A componente tangencial da aceleração relativa é sempre perpendicular ao vetor . E seu módulo pode ser calculado como:
Para calcular a componente normal da aceleração vamos usar:
Este componente tem a mesma direção do vetor , porém tem sentido oposto a ele. Seu módulo pode ser calculado como:
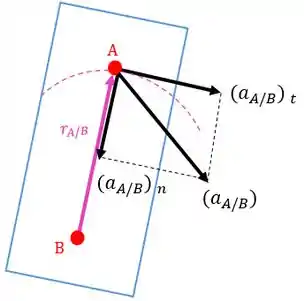
Então, a equação que vamos usar para resolver a maioria dos problemas de aceleração relativa é:
Esse sinal negativo vem do conceito de produto vetorial, não precisa se preocupar com isso!!!
Observações
Se estivermos tratando de corpos rígidos que possuem barras articuladas como esse aqui:

O ponto de contato entre as barras, neste caso é o ponto , terá a mesma aceleração na barra e na barra . Como o ponto faz um movimento curvil��neo, a sua aceleração terá duas componentes, a tangencial e a normal. Na barra , o ponto se move em uma trajetória reta, logo é horizontal.
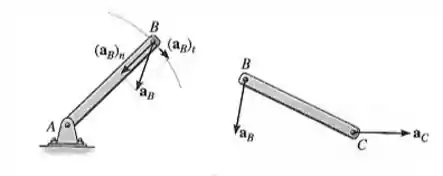
Se dois corpos estiverem só em contato entre si e eles se moverem em trajetórias diferentes, as componentes tangenciais das acelerações dos pontos serão iguais, mas as componentes normais serão diferentes. Isso ocorre em engrenagens, onde cada uma tem um movimento de rotação:
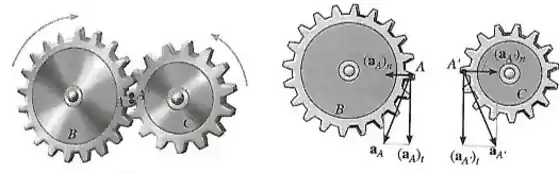
Vamos pegar o jeito fazendo exercícios. Partiu? ![]()
Observações
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 281-5/131
Determine a aceleração angular da barra e a aceleração linear de para se e nessa posição. Desenvolva sua solução usando notação vetorial.
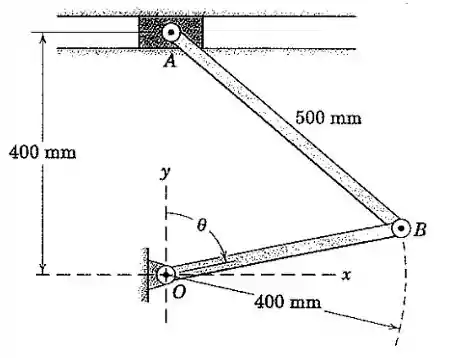
Passo 1
Vamos começar analisando as velocidades. Repare que as barras não possuem velocidade angular, pois foi dito no enunciado que :
Vamos ter que a velocidade do ponto será:
Como a velocidade angular é nula, vamos ter que:
Como o ponto realiza um movimento circular em torno do ponto , podemos calcular a velocidade deste ponto assim:
Opa, mas a velocidade angular da barra é zero. Então:
Passo 2
Agora vamos fazer a análise das acelerações. Quando vamos ter:
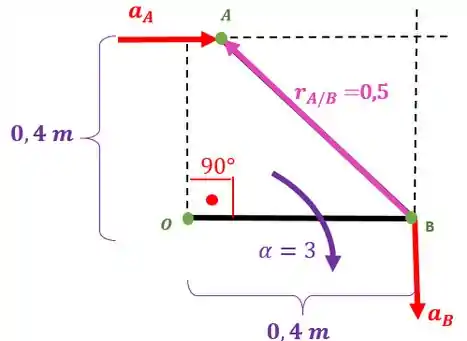
Podemos achar a aceleração do ponto , já que sabemos a aceleração angular da barra
Vetorialmente temos que o vetor aponta no sentido negativo do eixo :
Nossa equação da aceleração do ponto vai ser:
Como , então nos resta:
Passo 3
Vamos decompor nossos vetores no eixo para fazer a soma vetorial. Vamos começar pelo vetor :
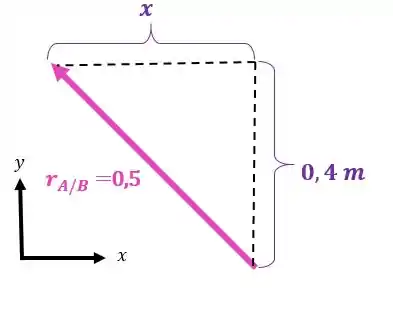
Por teorema de Pitágoras conseguimos achar o valor de :
Então, podemos escrever nosso vetor assim:
Sabemos que o vetor aceleração angular da barra está no eixo . Vamos arbitrar um sentido para ele e depois verificamos se está certo. Vamos colocar o vetor como positivo no eixo :
E o vetor aceleração do ponto (Esse é o vetor que queremos determinar, mas sabemos que ele está no eixo , pois o ponto só pode se mover na horizontal:
Então, vamos ter que:
Passo 4
Vamos fazer o produto vetorial:
Nossa matriz vai ficar:
Vamos substituir isso na nossa equação:
Agora é só separarmos as equações de acordo com suas componentes:
Da segunda equação podemos determinar o valor de :
O sinal negativo indica que escolhemos o sentido errado do vetor , ou seja, ele aponta no sentido negativo do eixo :
Pela primeira equação vamos achar o valor da aceleração no ponto :
Repare que o valor deu positivo, isso significa que o sentido que arbitramos para o vetor está certo. Ou seja, ele deve ficar assim:
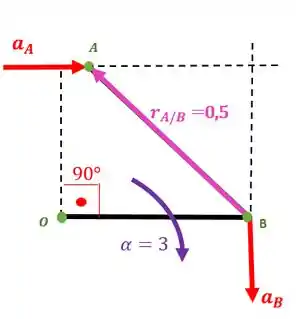
Resposta
Exercício Resolvido #2
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 280-5/127
A viga de aço de está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em e . Se as acelerações angulares iniciais dos tambores de elevação são e nos sentidos indicados, determine a aceleração angular correspondente da viga, a aceleração de , e a distância desde até um ponto sobre a linha de centro da viga que não possui aceleração.
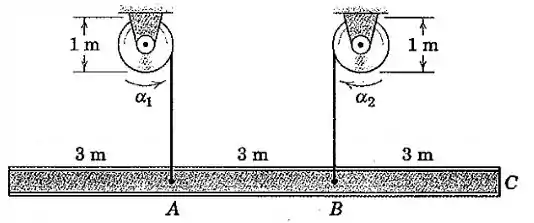
Passo 1
Vamos começar montando um esquema para entendermos o que está acontecendo:
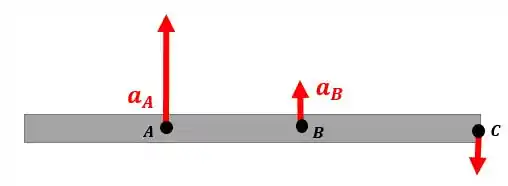
Repare que o ponto é puxado com uma velocidade maior que o ponto . Mas quando isso acontece o ponto acaba descendo, pois a viga tende a girar em torno do ponto que vamos chamar de :
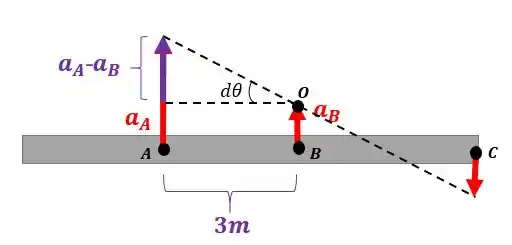
Podemos calcular a aceleração dos pontos e com os dados das suas respectivas polias:
E para o ponto :
Agora podemos achar a aceleração relativa de com relação a :
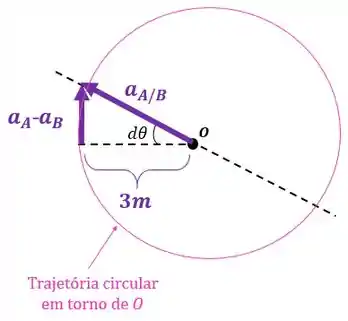
Repare que a viga tende a girar no sentido horário, então a aceleração angular é negativa (não esqueça da nossa convenção de positivo e negativo):
Passo 2
Como estamos analisando o movimento em torno de e sabemos que a viga gira com aceleração angular de , podemos calcular a aceleração do ponto usando nosso esquema:
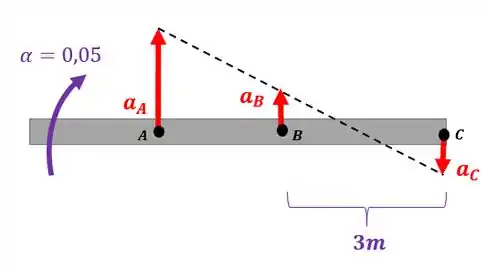
Vamos ter que:
Como est�� em sentido contrário a , temos que colocar um sinal negativo:
Repare que o sinal deu positivo, o que indica que o sinal que arbitramos para está correto, ou seja, ele aponta para baixo:
Passo 3
A questão pede a distância do ponto até um ponto de aceleração nula que passe pela linha de centro da viga:
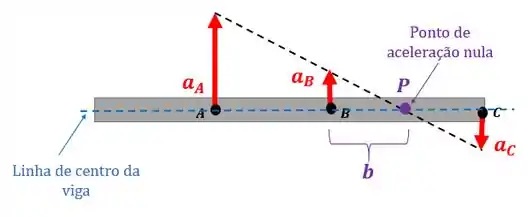
Para achar a distância é só usarmos o nosso esquema:
Sabemos que a aceleração no ponto é zero, então:
Resposta
Exercício Resolvido #3
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 291-16.113
O disco está se deslocando para a esquerda com aceleração angular e a velocidade angular . Se ele não escorrega em , determine a aceleração do ponto .
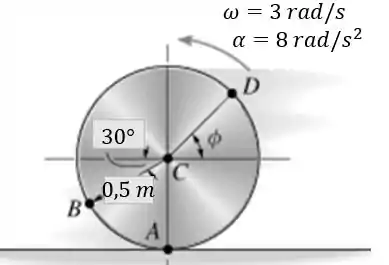
Passo 1
Nosso primeiro passo é relacionar o ponto que queremos saber as informações (ponto ) com um ponto que já temos algum dado ou que pelo menos conseguimos saber as informações dele de um jeito fácil.
O centro do disco vai ser o nosso ponto, pois sua aceleração será:
E quanto ao seu sentido? Como o disco não sofre uma desaceleração (a aceleração angular está no mesmo sentido da velocidade angular), então a aceleração do ponto está no sentido do movimento:
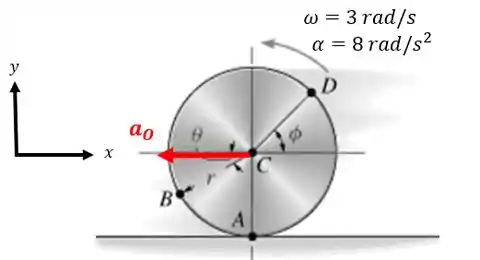
Então:
Feito isso, vamos montar nossa equação da aceleração:
Vamos ter o seguintes vetor :
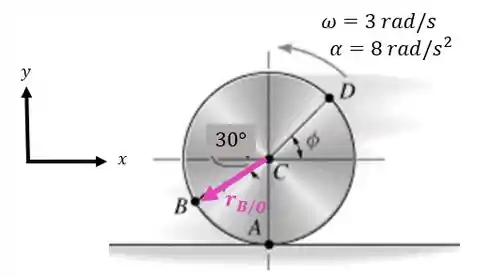
Vamos decompor os vetores para fazermos o produto vetorial. O vetor pode ser escrito como:
Repare que a aceleração do ponto é a resultante entre a aceleração tangencial e a normal:
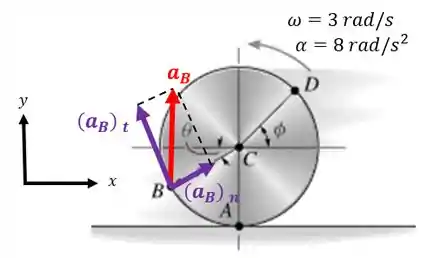
Então, podemos escrever o vetor aceleração do ponto em função de suas componentes e :
A aceleração angular e a velocidade angular fazem o disco girar no sentido anti-horário, ou seja, as duas são positivas de acordo com a nossa convenção de sinais:
Passo 2
Vamos substituir o que temos até agora na nossa equação:
Vamos ter que:
Vamos fazer o produto vetorial separado:
Agora é só substituir:
Vamos separar as equações de acordo com as componentes e :
Então, a componente da aceleração do ponto será:
E a componente será:
A resultante será:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 290-16.105
Num dado instante, o pé A da escada tem aceleração e velocidade , ambas para esquerda. Determine a aceleração do topo e a aceleração angular da escada, nesse instante.
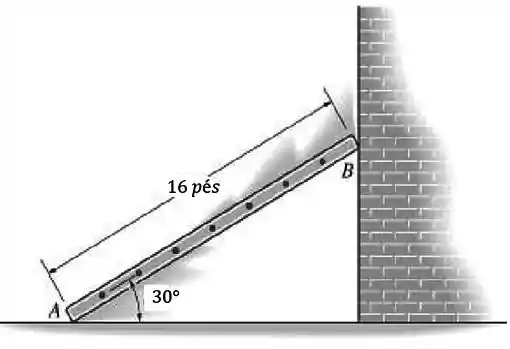
Passo 1
Vamos analisar inicialmente a velocidade do ponto , temos que:
Conforme o ponto vai para a esquerda, o ponto desce. Então, vamos ter que:
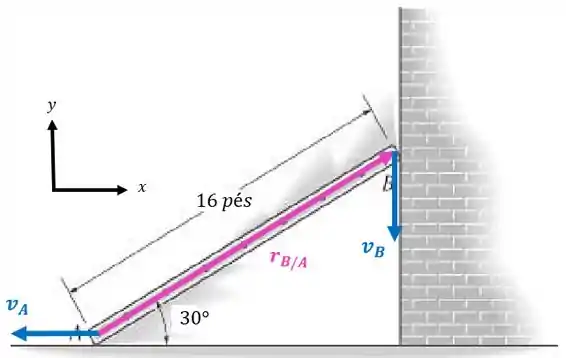
A velocidade será:
E podemos escrever a velocidade do ponto em termos de e :
A decomposição do vetor nos eixos e fica:
Repare que a barra tende a girar em torno do ponto e como este ponto se move para a esquerda, a barra tende a girar no sentido horário:
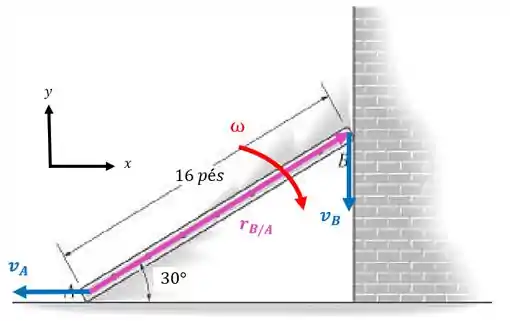
Então, pela convenção de sinais que adotamos, a velocidade angular desta barra é negativa:
Passo 2
Vamos fazer o produto vetorial agora:
Nossa matriz vai ficar:
Então, o que temos até agora é:
Vamos separar as nossas equações nas componentes e :
Opa, pela primeira equação conseguimos achar o valor da velocidade angular da barra:
Agora podemos achar o valor da velocidade no ponto usando a segunda equação:
Como tudo deu positivo, significa que arbitramos o sentido certo tanto para (sentido horário) quanto para (apontando para o sentido negativo do eixo ).
Passo 3
Agora vamos analisar as acelerações:
Repare que a aceleração do ponto será no mesmo sentido da velocidade, pois não está acontecendo uma desaceleração:
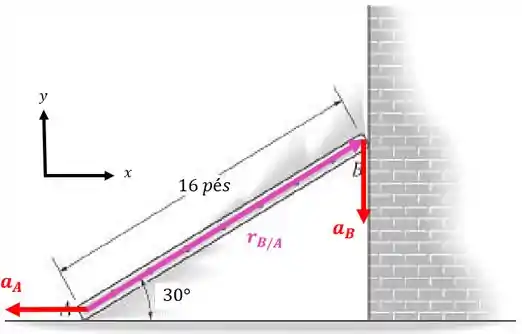
Temos que a aceleração do ponto é:
E a aceleração do ponto pode ser escrita assim:
Então, como fica a nossa equação:
Vamos ter que:
Repare que a aceleração angular da barra aponta no sentido horário também, assim como a velocidade angular. Isso porque a barra não sofre desaceleração:
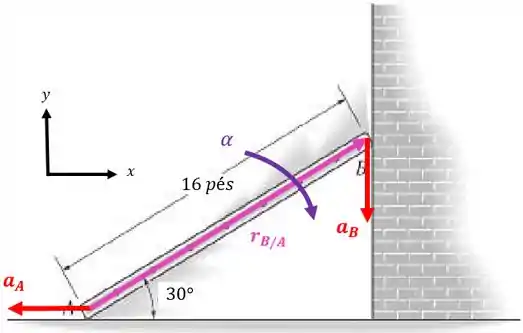
Então, podemos escrever a aceleração angular em função das suas componentes:
Vamos fazer o produto vetorial:
Vamos substituir isso na nossa equação da aceleração:
Agora, vamos separar nossa equação nas componentes e :
Da primeira equação conseguimos achar o valor da velocidade angular:
E substituindo isso na segunda equação obtemos o valor da aceleração do ponto :
O sinal positivo que achamos tanto para a aceleração angular quanto para a aceleração do ponto indica que arbitramos o sentido correto para esses vetores.
Resposta
Exercício Resolvido #5
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 291-16.112
Num dado instante, o volante está girando com a velocidade e a aceleração angulares indicadas na figura. Determine a aceleração do bloco , nesse instante.
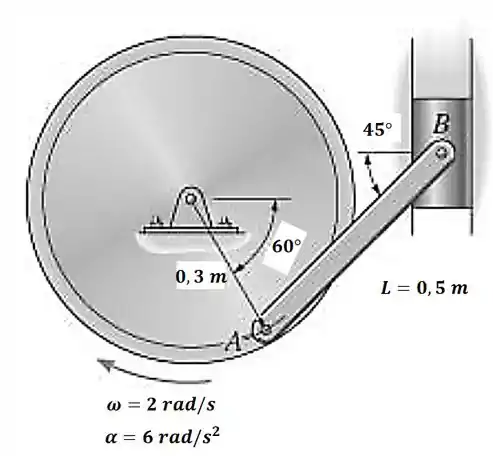
Passo 1
O que queremos saber é a aceleração do ponto , então vamos escrever a nossa equação da aceleração relativa assim:
Repare que não sabemos a aceleração angular da barra , mas podemos usar a equação da velocidade do ponto para achá-la:
A posição é:
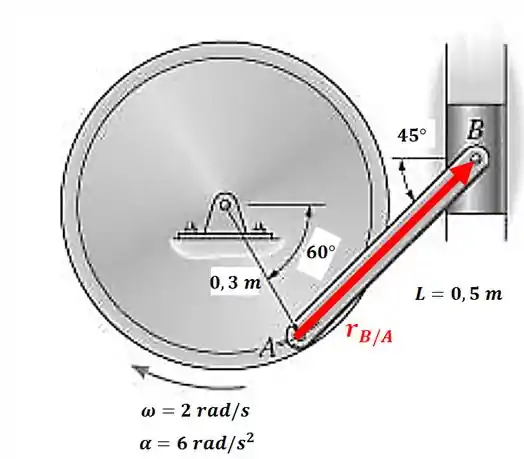
A velocidade do ponto podemos achar pela equação:
A velocidade angular do volante é negativa, pois está girando no sentido horário:
E a posição do ponto com relação ao centro do volante é:
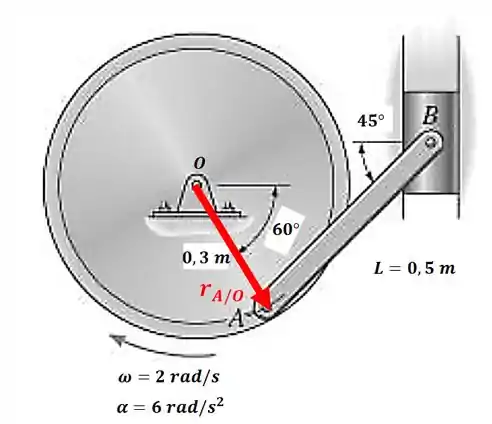
Então, a velocidade do ponto será:
Resolvendo esse produto vetorial temos:
Passo 2
Agora sim podemos achar o valor da velocidade angular da barra usando a equação da velocidade do ponto :
Repare que o ponto só pode se mover no eixo , então vamos arbitrar a velocidade como positiva:
E vamos arbitrar o sentido da velocidade angular da barra como positivo:
Então, o produto vetorial fica:
Substituindo isso na nossa equação:
Agora vamos somar os termos de mesma componente:
Da equação em podemos achar o valor de :
Como o resultado deu negativo, significa que arbitramos o sentido contrário:
Como não vamos precisar do valor de , vamos deixa-lo pra lá!
Passo 3
O que queremos saber é a aceleração do ponto , certo? Então, vamos resgatar a equação lá do início:
Vamos substituir o que já temos:
Ou seja, precisamos achar a aceleração do ponto e a aceleração angular da barra .
Vamos começar pela aceleração do ponto :
Sabemos que a velocidade angular do volante é negativa, pois está girando no sentido horário:
Então:
Resolvendo o produto vetorial temos:
Substituindo isso vamos ter:
E a aceleração angular da barra vamos arbitrar como positiva:
Passo 4
Agora vamos substituir essas coisas na equação da aceleração do ponto :
Repare que o ponto só pode se mover na vertical, então a sua aceleração é:
Vamos arbitrar como positiva!
Então, vamos ter que:
Vamos resolver o produto vetorial:
Substituindo isso aí na nossa equação:
Agora vamos separar as componentes:
Da primeira equação podemos determinar o valor de :
E finalmente podemos achar o valor da aceleração do ponto :
Então:
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 293-16.128
O bloco deslizante move-se para a direita com aceleração de . Na situação mostrada na figura, a velocidade de é de . Determine a aceleração angular da barra e a aceleração do ponto , na situação considerada.
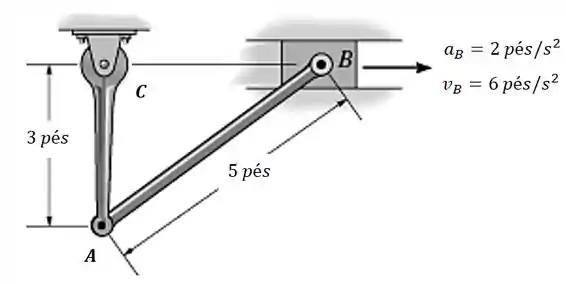
Passo 1
Vamos começar resolvendo esta questão relacionando os pontos e , pois temos alguma informação sobre o movimento do ponto . Podemos relacionar a velocidade destes pontos usando a seguinte equação:
A velocidade do ponto foi dada e vale:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar como positiva:
E o vetor posição relativa é:
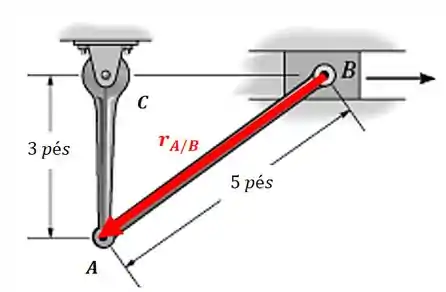
Vamos ter o seguinte triângulo retângulo:
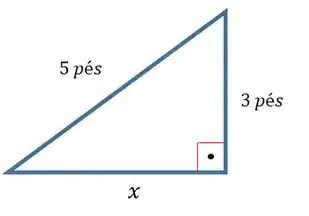
Usando o Teorema de Pitágoras conseguimos achar o valor de :
Então, o vetor posição será:
Agora que já identificamos cada termo da equação é só substituirmos:
Esse produto vetorial fica:
Substituindo isso na nossa equação:
Mas somente com esta equação não conseguimos determinar o valor da velocidade do ponto , temos que arranjar outro jeito de achar a velocidade deste ponto.
Passo 2
Outra forma de achar a velocidade do ponto é usarmos a barra :
Repare que o ponto gira em torno do ponto que está fixo. Dessa maneira, a velocidade do ponto é zero:
Nós não sabemos o valor da velocidade angular da barra , mas vamos arbitrar seu sentido como positivo:
E o vetor posição será:
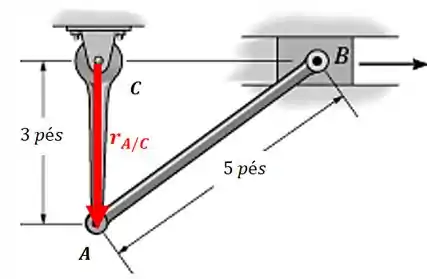
Substituindo na nossa equação:
Resolvendo esse produto vetorial obtemos:
Agora vamos resgatar a outra equação para determinar a velocidade do ponto :
Igualando as duas, temos que:
Agora vamos separar as equações de acordo com as componentes e :
Da segunda equação tiramos que:
E da primeira equação temos que:
Como o valor deu positivo, significa que arbitramos o sentido correto:
Passo 3
Agora vamos relacionar as acelerações dos pontos e :
Já sabemos que:
E que:
Não sabemos o valor da aceleração angular da barra , mas vamos arbitrar como positiva:
Substituindo tudo isso na nossa equação, temos que:
Resolvendo o produto vetorial, temos que:
Então, nossa equação fica:
Vamos guardar esta informação, porque só com ela não conseguimos avançar na questão.
Passo 4
Vamos usar a barra para termos outra equação para a aceleração do ponto . Como o ponto gira em torno de um ponto fixo, podemos escrever:
Já sabemos desta equação que:
E:
Nós não sabemos a aceleração angular, mas vamos arbitrá-la como positiva:
Substituindo tudo isso, temos que:
Resolvendo o produto vetorial:
Então, nossa equação fica:
Passo 5
Nosso próximo passo é igualar as duas equações para aceleração do ponto que temos:
E:
Então, vamos ter que:
Vamos separar as equações de acordo com as componentes e :
Da segunda equação obtemos que:
Como achamos um valor negativo, significa que arbitramos o sentido contrário para a aceleração angular da barra :
Essa é a nossa primeira resposta. Falta acharmos a aceleração do ponto .
Para isso, vamos resgatar a equação que já montamos anteriormente:
Temos que:
Esse produto vetorial fica:
Então:
E o seu módulo fica:
Vamos achar também o ângulo de inclinação deste vetor. Para isso, vamos desenhá-lo:
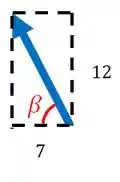
Temos que:
Então:
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Dinâmica: Mecânica para Engenharia, 10º ed. SP: Prentice Hall, 2005, pp. 293-16.127
Determine a aceleração angular da barra de ligação , considerando que a barra tem a velocidade e a desaceleração angulares indicadas na figura.
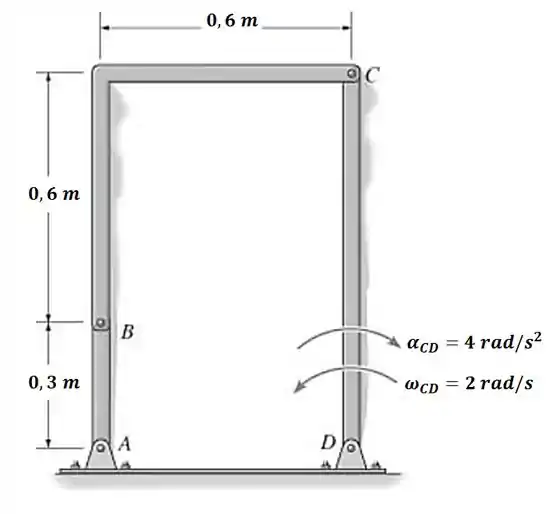
Passo 1
Vamos começar resolvendo esta questão pela barra , pois temos alguma informação sobre seu movimento. Repare que o ponto realiza um movimento em torno do ponto que está fixo, então podemos dizer que:
Sabemos que a barra possui uma desaceleração, então:
Já a sua velocidade angular é positiva, pois está girando no sentido horário:
E o vetor posição ?
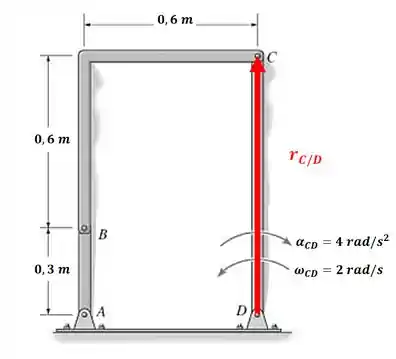
Então:
Agora que identificamos cada termo da nossa equação, é só substituirmos tudo:
Vamos resolver este produto vetorial:
Então:
Passo 2
Agora vamos achar a velocidade do ponto :
Repare que o ponto está fixo, então sua velocidade é nula:
Portanto:
Resolvendo este produto vetorial, vamos ter que:
Repare que o produto vetorial de uma componente em e outra em sempre resulta em uma componente em . ![]()
Passo 3
Vamos partir para a barra . Repare que o ponto gira em torno do ponto que está fixo, então:
Como o ponto é fixo, sua velocidade é nula:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar que ela esteja no sentido positivo:
E o vetor posição ?
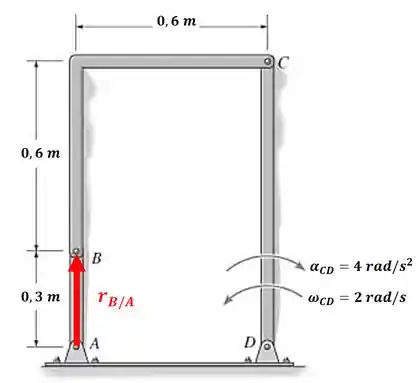
Como já definimos o que é cada termo da nossa equação, vamos substituir as coisas:
Resolvendo este produto vetorial, vamos ter que:
Vamos guardar esta informação e tentar outra maneira de achar a velocidade do ponto .
Passo 4
Agora vamos relacionar os pontos e para acharmos a velocidade do ponto , já que temos informações sobre o ponto :
Vamos identificar o que é cada termo desta equação.
A velocidade do ponto nós já calculamos:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar como positiva:
E o vetor posição relativa será:
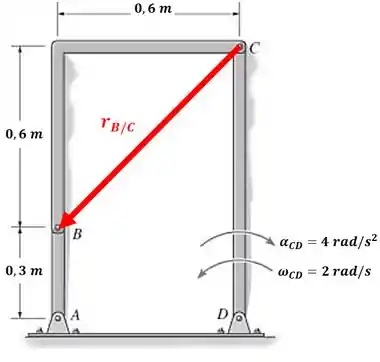
Pronto! Agora é só substituir:
Resolvendo este produto vetorial:
Então, vamos ter que:
Beleza?
Lembra que eu falei para guardarmos a informação que tínhamos sobre a velocidade do ponto ? Vamos resgatá-la agora:
E substituir ela na nossa equação:
Agora vamos separar as equações de acordo com as componentes e :
Da equação em tiramos que a velocidade angular da barra é zero:
E da primeira equação, temos que:
Como a velocidade angular da barra deu positiva, significa que arbitramos o sentido correto para ela:
Passo 5
Agora vamos relacionar o ponto e para achar a aceleração. Como esses dois pontos se movem, temos que:
O que não sabemos dessa equação é a aceleração do ponto () e a aceleração angular da barra . Vamos arbitrar o sentido positivo para a aceleração angular da barra :
Pronto! Vamos substituir tudo o que temos:
Não esqueça que a velocidade angular da barra é zero!
Vamos resolver o produto vetorial:
Substituindo na nossa equação, temos que:
Vamos guardar essa informação e arranjar outro jeito de achar a aceleração do ponto !
Passo 6
Outra forma de achar a aceleração do ponto é usando a barra . Como o ponto gira em torno de um ponto fixo (ponto ) vamos ter que:
Nós já determinamos antes que:
E:
Falta a aceleração angular da barra () e é exatamente isto que a questão quer saber!
Vamos arbitrar o sentido positivo para ela:
E agora podemos substituir tudo:
Como já estamos craques em produto vetorial, vamos ter que:
Então, a nossa equação fica:
Lembra o que sabemos sobre aceleração do ponto ?
Vamos substituir isso na nossa equação lá de cima:
Agora é só separarmos as equações de acordo com as componentes e :
Resolvendo a segunda equação, temos que:
Substituindo isso na primeira equação temos que:
Como achamos um valor negativo para a aceleração angular da barra , significa que arbitramos o sentido contrário para ela. Então, ela está girando no sentido horário: