Movimento Restrito
Produzido por Pablo RicardoTeoria
Introdução
Você já aprendeu um pouco sobre o movimento dos corpos. Aprendeu, inclusive, a analisar dois movimentos e verificar qual é a velocidade relativa entre eles.
Agora imagine um caso em que dois corpos estejam conectados entre si de modo que o movimento de um deles afeta o movimento do outro. Tipo assim:
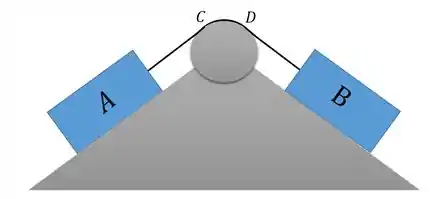
Repare que se o bloco A descer o plano inclinado, o bloco B irá subir do outro lado, não é mesmo?
Como calcular a velocidade relativa neste caso?
É isso que iremos aprender neste capítulo. Então, vamos lá...
Movimento Restrito
Em alguns casos, o movimento de um corpo depende do movimento de outro corpo. Isso geralmente ocorre quando os pontos estão interligados por cordas ou cabos que passam por roldanas.
Vamos analisar o seguinte sistema:
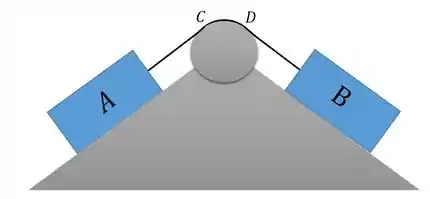
Nós vimos que se o bloco estiver descendo o plano inclinado, o bloco estará subindo do outro lado do plano, pois existe uma corda que conecta esses dois blocos.
Podemos descrever o movimento desse sistema analisando as posições de cada bloco com relação a um ponto de referência fixo que neste caso vamos considerar o centro da roldana:
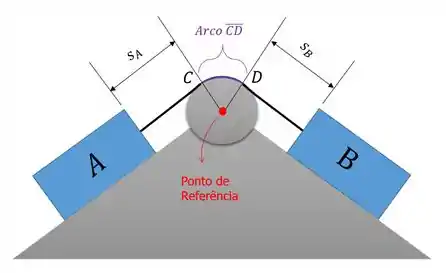
O comprimento total () da corda que está ligando os dois blocos vai ser:
Velocidade e Aceleração
Perceba que quando o bloco desce o plano inclinado, o comprimento aumenta e ao mesmo tempo o comprimento diminui, já que o comprimento total da corda é constante.
E o que temos aqui? Uma variação da posição dos blocos com o passar do tempo. É exatamente isso que você está pensando... Temos uma derivada da posição com relação ao tempo:
Repare que o comprimento total da corda e o comprimento do não mudam e derivada de constante é zero, então vamos ficar com:
A derivada da posição com relação ao tempo é o que mesmo? A velocidade...
Ou ainda:
Esse sinal negativo indica que a velocidade do bloco é para baixo enquanto que a velocidade do bloco é para cima, ou seja, elas tem sentidos opostos.
E a aceleração? É só derivarmos de novo a equação da velocidade:
Agora vamos ver um exemplo um pouco mais complexo...
Vamos determinar a velocidade do corpo sabendo que o corpo está subindo com uma velocidade .
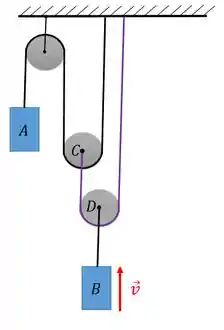
Nosso primeiro passo vai ser escolher um ponto ou eixo de referência. Repare que não temos um ponto fixo entre os dois bloquinhos para ser usado como ponto de referência, então vamos fazer um eixo.
Vamos passar o eixo de referência pela roldana que está fixa ao teto e estabelecer os sentidos positivos pelo eixo :
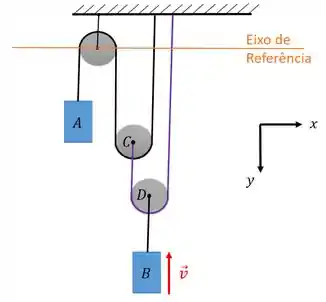
Agora vamos localizar a posição de todos os elementos a partir do eixo de referência que escolhemos.
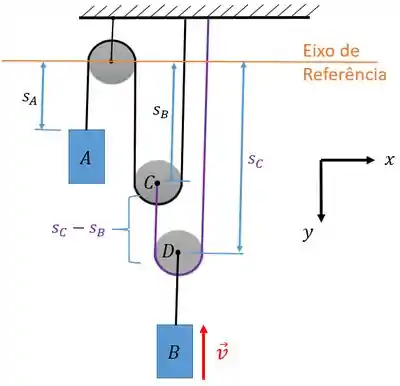
Repare que esse sistema tem duas cordas separadas uma preta e outra roxa. E o que isso significa? Que vamos ter duas equações de comprimento total, uma para cada corda.
Vamos chamar de o comprimento total da corda preta:
Sacou o motivo de ter um 2 na frente de Se você olhar a figura, vai ver que precisa ser contado duas vezes por causa da roldana: uma vez para cada lado.
E vamos chamar de o comprimento total da corda roxa:
Como vimos no exemplo inicial, não precisamos contar os trechos da corda em contato com as roldanas, pois esses valores são constantes e quando derivarmos vai dar zero.
Agora precisamos transformar essas duas equações em uma única. Qual o termo em comum entre as duas equações? É o ... Então vamos isolá-lo em cada equação:
Agora vamos igualar as duas equações:
Como o problema quer saber a velocidade, então vamos derivar essa equação que achamos com relação ao tempo:
Como os comprimentos e não mudam, então a derivada desses termos vai ser zero:
Então:
Como a velocidade do corpo é a mesma velocidade na roldana , então podemos dizer que:
Maaas... Lembra que o nosso sentido positivo de está apontando para baixo? A velocidade está apontando para cima, ou seja, está no sentido negativo. Então, na verdade:
Sacou? Então a velocidade do bloco A será de:
Show!!! Para os próximos exercícios você vai seguir esse mesmo raciocínio.
Então vamos praticar para pegar o jeito!!!
Velocidade e Aceleração
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 75, 2/213
Se o bloco tem um velocidade de para a direita, determine a velocidade do cilindro .
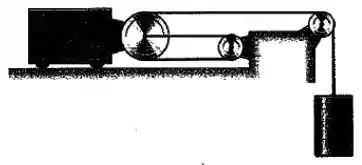
Passo 1
Pela geometria do sistema, podemos dizer que o comprimento total da corda pode ser aproximado por:
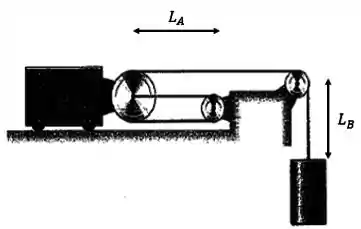
No entanto, temos que levar em consideração as “voltinhas” nas roldanas. Como não sabemos os diâmetros das roldanas, vamos dizer que será:
Onde é uma constante desconhecida (ela vai sumir nos próximos passos).
Passo 2
Derivando a expressão de em relação ao tempo, vamos ter que:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 75, 2/216
Determine a equação de restrição que relaciona as acelerações dos corpos e . Assuma que a superfície superior de permanece na horizontal.
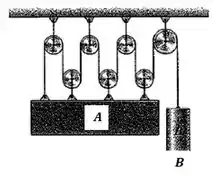
Passo 1
O sistema é dado por:
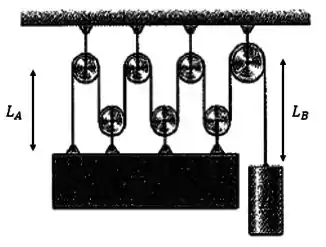
Assim, como fizemos na questão anterior, o comprimento total da corda será dado por:
é a constante que representa os comprimentos das circunferências das roldanas.
Passo 2
Assim, derivando a expressão de vamos ter que:
Derivando de novo:
E essa é a equação de restrição.
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 75, 2/215
Em um dado instante, o cilindro tem uma velocidade para baixo de e uma aceleração para cima de . Determine a velocidade e a aceleração correspondentes do cilindro .
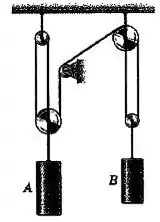
Passo 1
O sistema pode ser descrito por:
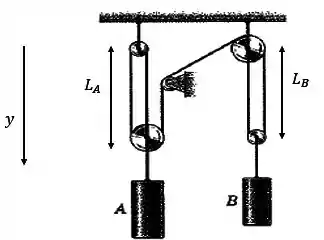
Observe que o sentido positivo do eixo aponta para baixo, ou seja, esse é o sentido positivo para o deslocamento.
A gente pode notar que existem dois comprimentos , certo?
Mas devemos computar quantos comprimentos ? Bom, de cara vemos 2... mas são
Naquela parte que existe uma roldana:
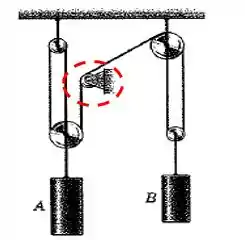
O comprimento da corda que vai de até a outra roldana tem, pelo menos, um valor . Assim, podemos dizer que:
Onde é a constante que engloba todos os comprimentos desconhecidos.
Passo 2
Assim, se derivarmos uma vez:
Derivando de novo:
Assim, a velocidade de será:
E a aceleração:
Por que é negativo? Porque está apontando para cima. Assim:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 76, 2/220
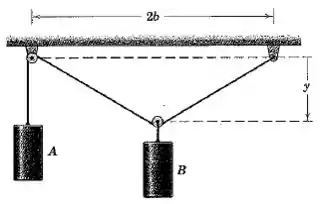
Para um dado valor de , determine a velocidade ascendente de em termos da velocidade descendente de . Despreze os diâmetros das polias.
Passo 1
Vamos olhar o sistema:
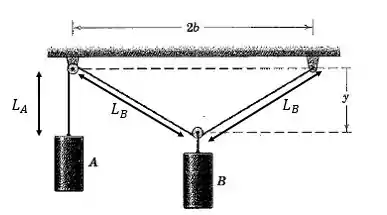
Assim:
Mas quem é
é:
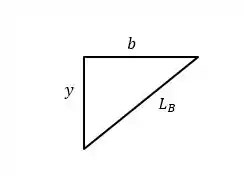
Assim:
E:
Passo 2
Derivando a expressão de :
Como derivar Devemos usar a regra da cadeia:
Assim:
Vamos chamar de
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 78, 2/228
Os anéis e deslizam ao longo das hastes fixas em ângulo reto e estão conectados por um fio de comprimento . Determine a aceleração do anel em função de se o anel possui uma velocidade contante para cima .
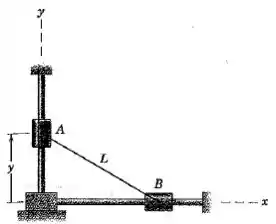
Passo 1
O sistema pode ser simplificado na seguinte figura:
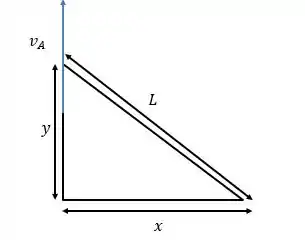
E quem é é dado por:
Passo 2
tem que satisfazer a seguinte equação:
Derivando em relação ao tempo:
E aí temos as relações das velocidades. Só que nós queremos a aceleração, né? Então, vamos derivar mais uma vez:
Sacou? Usamos a regra do produto. Simplificando:
Só que:
Por que? Porque o enunciado disse que a velocidade do anel é constante, assim a sua aceleração é nula.
E:
Então:
E quanto vale Podemos descobrir usando a primeira relação:
Passo 3
Assim:
Então:
Só que:
Passo 4
Beleza, estamos quase lá.
Lembrando que:
Assim:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2013, 77, 2/226
Os guinchos motorizados colocados no chão permitem que o andaime industrial seja elevado ou abaixado. Para a rotação no sentido indicado, o andaime está sendo elevado. Se cada tambor tem um diâmetro de e gira na taxa de , determine a velocidade de subida do andaime.
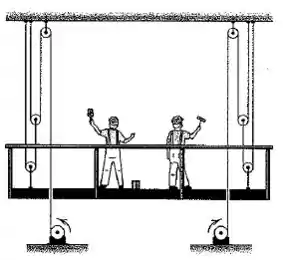
Passo 1
O sistema pode ser esquematizado por:
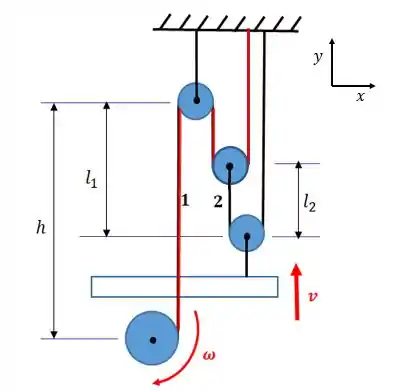
Vamos dividir o sistema em duas cordas: A corda vermelha que começa no tambor e termina no teto, e a corda preta que começa na roldana 2 e termina no teto também.
Para a corda vermelha vamos ter que:
Passo 2
Derivando a expressão que achamos, temos que:
Só que:
Assim:
Passo 3
Já o comprimento da corda vermelha é o seguinte:
Assim:
Quando o andaime sobe, o comprimento diminui na mesma proporção, assim:
Assim:
Beleza?
Passo 4
Assim:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 78, 2/221
Despreze os diâmetros das pequenas polias e determine a relação entre a velocidade de e a velocidade de para um determinado valor de .
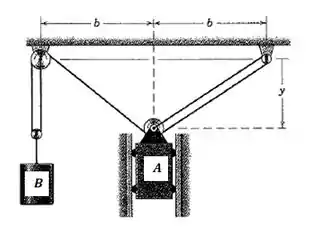
Passo 1
O sistema pode ser desenhado assim:
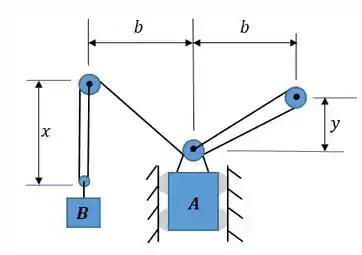
Passo 2
Assim:
Derivando essa expressão, temos que:
Adotando:
Então: