Movimento Relativo
Produzido por Pablo RicardoTeoria
Introdução
Imagine que você está andando de carro a e tem outro carro, do seu lado, que está andando a também:

Para um observador na beira da estrada, vocês estão se deslocando bem rapidamente. No entanto, você olha por sua janela e vê que o carro vizinho parece estar parado.
Como explicar isso?
É o que vamos aprender neste capítulo! Partiu?
Movimento Relativo
Imagine dois corpos e se movendo:
Vamos analisar o movimento que faz com relação a . Para isso, imagine que você vai se posicionar em cima do ponto e vai observar tudo que está fazendo.

Para analisar o ponto vamos precisar fixar um eixo com a origem bem em cima do ponto B e chamá-lo de eixo móvel :
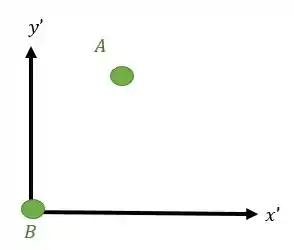
Nesse eixo, vamos ter o vetor posição do corpo medido em relação ao corpo :
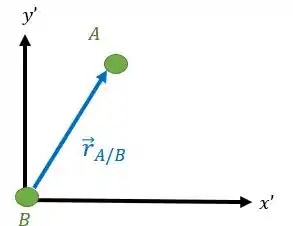
Onde, e são os vetores unitários ao longo do eixo e é a posição relativa entre .
Este vetor indica como o corpo está posicionado quando você o observa a partir do ponto . Observe que o vetor começa na origem do eixo móvel e chega no ponto que estamos analisando que é o corpo .
Agora, temos que achar a posição absoluta dos pontos e . Mas o que seria posição absoluta? É aquela posição medida a partir de um eixo fixo localizado em um ponto de referência. Vamos chamar este eixo de eixo absoluto e posicioná-lo fora dos pontos:
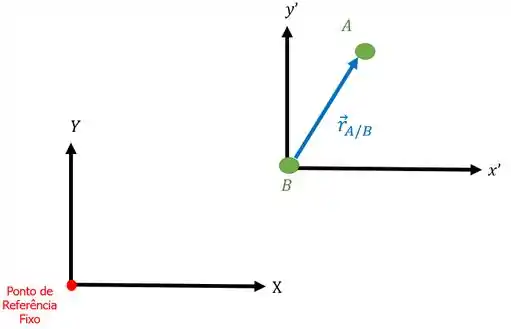
Depois que posicionamos nosso eixo absoluto em um ponto de referência, podemos achar os vetores posição do corpos e com relação a este eixo, assim:
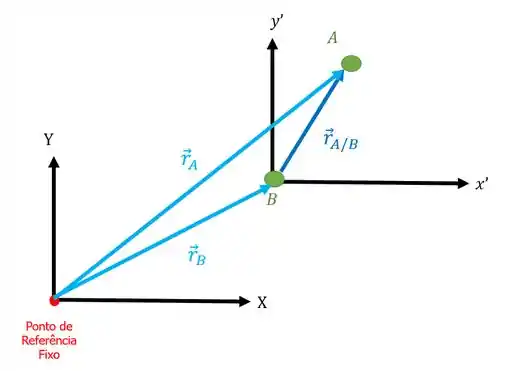
Perceba que os vetores e começam na origem do eixo absoluto e chegam no respectivo ponto.
Se retirarmos os eixos vamos ter o seguinte:
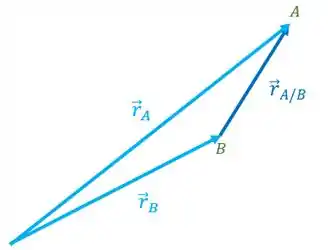
É uma soma de vetores!!! E podemos obter a seguinte equação:
O que essa equação nos diz? Que a posição absoluta do corpo é igual a posição absoluta do corpo mais a posição relativa de com relação a .
E se for igual a ?
E isso quer dizer que os pontos estão na mesma posição!!!
Velocidade
E se quisermos saber a velocidade com que o corpo se move com relação ao corpo ? É só lembrar que a velocidade é a derivada da posição com relação ao tempo, então...
O que é a mesma coisa que:
Isso quer dizer que a velocidade do corpo é igual a velocidade do corpo mais a velocidade do corpo com relação a .
Sabendo disso agora, por que o carro que estava do nosso lado lááá no exemplo do início do capítulo parecia estar parado?
Porque a velocidade de era igual a velocidade de , então:
Ou seja, a velocidade relativa entre eles é nula. Isso quer dizer que para os observadores dentro de um dos carros o outro carro está parado.
Aceleração
E a aceleração? Só fazermos o mesmo procedimento e derivarmos a equação da velocidade com relação ao tempo:
O que é a mesma coisa que:
Mudando o observador
Você deve estar se perguntando: e se eu quiser fazer ao contrário e analisar o movimento que o corpo tem em relação ao corpo ? É muito simples, é só colocar o eixo móvel com a origem em :
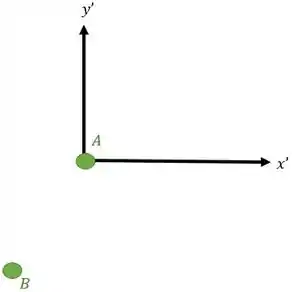
E achar o vetor posição relativa sempre começando na origem do eixo e chegando no ponto que estou analisando:
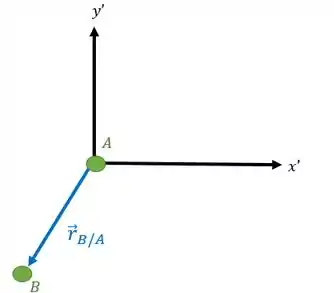
Repare numa coisa muito importante: o nome do vetor mudou. Agora o vetor posição é e não mais . Isso é muito importante!!!
O vetor indica a posição do corpo com relação ao corpo .
Vai aí uma dica para você não errar mais:

Show!!!
Vamos continuar no nosso caso em que o eixo móvel está posicionado bem em cima do corpo ....
Ficou faltando acharmos a posição absoluta dos corpos:
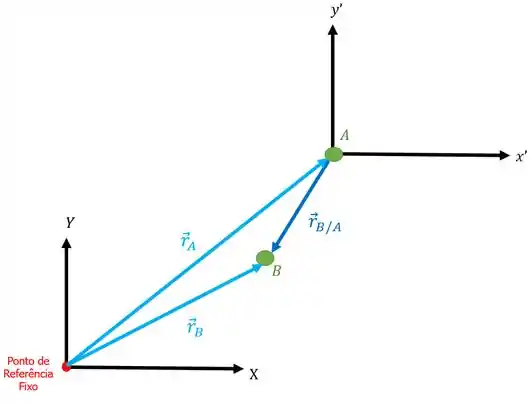
Repare novamente que o vetor sempre começa na origem do eixo.
Vamos ter o seguinte:
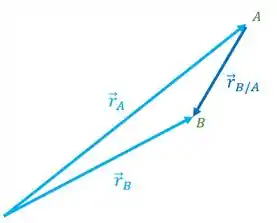
Somando os vetores vamos ter a seguinte equação:
Repare que antes do sinal de igual vem a posição do corpo que estou analisando que é o . Isso também é importante!!!
Para sabermos a velocidade é só derivarmos a equação acima:
E o mesmo processo para a aceleração:
Beleza! Partiu praticar nos exercícios?
Velocidade
Aceleração
Mudando o observador
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 69, 2/190
O jato de transporte está voando para o norte com uma velocidade quando uma aeronave menor passa por baixo do transporte dirigida na direção mostrada. Para os passageiros em , no entanto, aparenta estar voando lateralmente e movendo-se para leste. Determine a velocidade real de e a velocidade que aparenta ter em relação a .
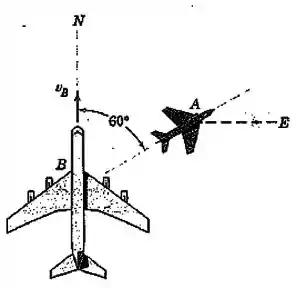
Passo 1
A velocidade que aparente ter para é a nossa velocidade relativa .
Quando o enunciado nos diz que ela parece ser lateral para , quer dizer que o ângulo que ela faz com a horizontal é nulo.
Mas a velocidade “real” de faz um ângulo de com a vertical. Assim, podemos montar o seguinte esquema vetorial:
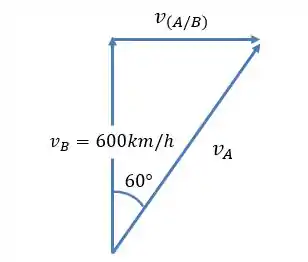
Passo 2
A questão praticamente acabou! Basta a gente usar apenas as relações trigonométricas:
E:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 69, 2/192
O trem viaja com uma velocidade constante ao longo da estrada de ferro reta e horizontal. O motorista do carro , antecipando a passagem de nível ferroviária , diminui a velocidade do carro de na taxa de . Determine a velocidade e a aceleração do trem em relação ao carro.
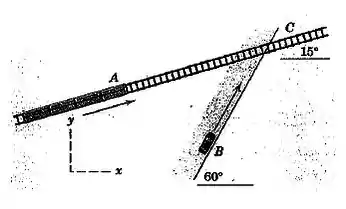
Passo 1
A velocidade do trem, , pode ser escrita como:
Assim, a velocidade relativa de em relação a é:
Passo 2
Podemos escrever o vetor usando o ângulo de
E o
Assim:
Passo 3
A aceleração relativa será calculada da mesma forma:
Sendo que a aceleração do trem é nula: .
E:
Por que negativo? Porque é uma desaceleração. Está agindo no sentido contrário ao movimento de
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 69, 2/193
Para o instante representado, o carro tem uma velocidade de , que está aumentando na taxa de cada segundo. Simultaneamente, o carro também tem uma velocidade de enquanto contorna a curva e está reduzindo a velocidade na taxa de cada segundo. Determine a aceleração que o carro aparenta ter para um observador no carro .
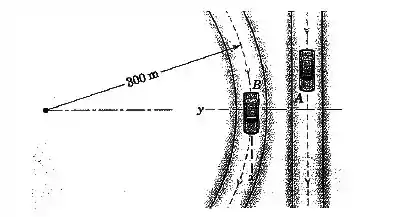
Passo 1
Vamos primeiro analisar o carro
O enunciado diz que a velocidade do carro aumenta em a cada segundo. Essa é a aceleração:
Passo 2
Agora vamos analisar
O carro tem uma aceleração tangencial, já que a sua velocidade diminui, e uma centrípeta, já que faz uma curva:
A sua velocidade no instante considerado vale:
E a aceleração centrípeta:
Passo 3
Colocando todos os vetores em um mesmo plano:
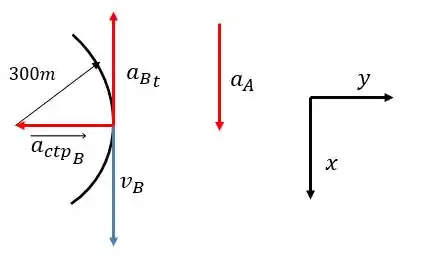
Escrevendo o vetor
O vetor
Assim, usando a nossa velha fórmula:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 70, 2/195
O carro tem uma velocidade para a frente de e está acelerando a . Determine a velocidade e a aceleração do carro em relação ao observador , que é levado em uma cadeira sem rotação sobre a roda-gigante. A velocidade angular da roda-gigante é constante.
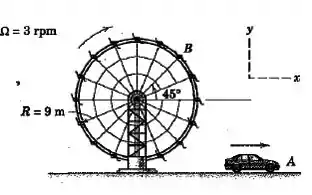
Passo 1
Novamente, vamos usar:
Onde é a velocidade relativa entre os móveis.
Passo 2
Bom, a velocidade do carro é, em
Passo 3
A frequência de rotação está em . Para transformar para , basta dividir por
E a velocidade angular é:
Passo 4
A velocidade tem uma direção dada por:
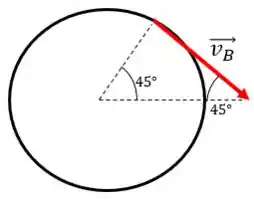
Quanto vale o módulo de ? Ele é dado por:
Assim:
Por que o sinal negativo em Porque a velocidade está com a componente vertical apontando para baixo.
Assim, podemos dizer que:
Passo 5
A única aceleração do móvel é a aceleração centrípeta:
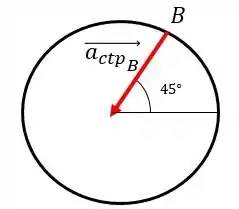
Seu módulo é dado por:
E:
E a aceleração de
É só:
Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 72, 2/206
O avião está voando horizontalmente com uma velocidade constate de e está rebocando o planador , que está ganhando altitude. Se o cabo de reboque tem um comprimento e está aumentando na taxa constante de graus por segundo, determine os módulos da velocidade e da aceleração do planador para o instante em que .
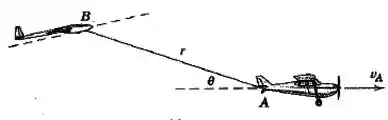
Passo 1
Opa, vamos começar essa questão com uma reflexão: os dois aviões estão conectados por uma corda, certo?
O comprimento da corda se altera?
Não!
O que é relativo entre os dois aviões e se altera com o tempo?
O ângulo entre eles, que cresce a uma taxa de .
Passo 2
Sabemos que:
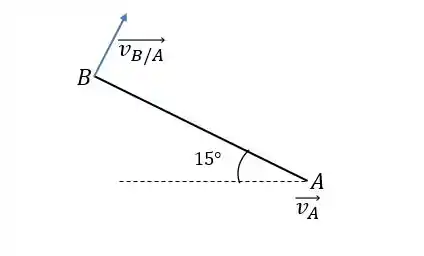
E como comentamos, a velocidade relativa entre e tem a ver com a variação angular. Podemos escrever:
Assim:
Passamos pra radianos, tá vendo?
Agora:
Passo 3
Bom, como o ângulo na horizontal vale , o ângulo entre e vale :
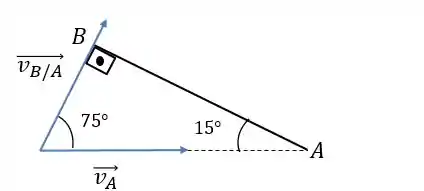
Assim, pra somarmos os vetores e vamos usar a regra do paralelogramo:
A velocidade em será:
Assim:
Passo 4
Só que:
Então:
E quem é Como está girando em torno de , essa vai ser a aceleração centrípeta:
Assim:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 72, 2/206
Os trens e circulam sobre vias paralelas. O trem tem uma velocidade de e está diminuindo na taxa de , enquanto o trem tem uma velocidade constante de . Determine a velocidade e a aceleração do trem em relação ao trem .
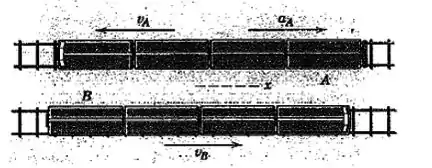
Passo 1
Essa é bem simples:
Temos que:
E:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 72, 2/198
Um veleiro deslocando-se na direção mostrada está navegando a barlavento contra um vento norte. O instrumento que mede a velocidade do barco registra uma velocidade do casco de nós. Uma corda leve amarrada ao cordame indica que a direção do vento aparente é de a partir da linha de centro do barco. Qual é a velocidade do vento ?
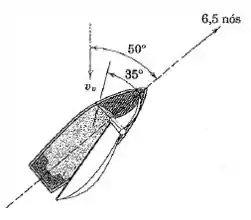
Passo 1
Podemos esquematizar o sistema de vetores por
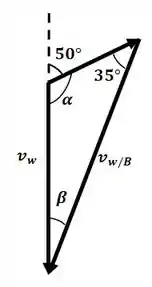
Temos que o ângulo é:
E com isso podemos determinar o ângulo :
Passo 2
Temos:
Assim, podemos escrever:
E pela lei dos senos: