Forças em Três Dimensões
Teoria
Introdução
Imagine que você está dentro de um avião e de repente ele começa a passar por uma turbulência... Na turbulência, o avião sofre a ação de forças vindas de várias direções, sendo causadas pela movimentação do ar, além da ação do próprio peso do avião:
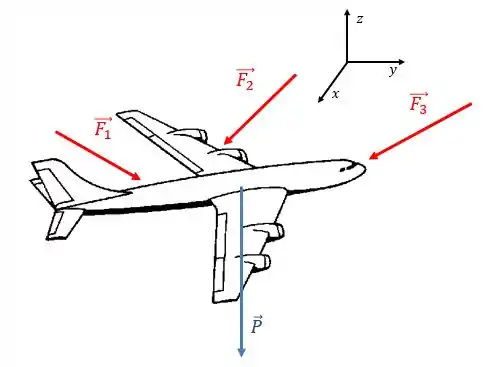
Você acha que dá para tratar esse problema da forma como estamos acostumados, ou seja, em duas dimensões?
Não!!!! Por isso vamos expandir nossos conhecimentos para o mundo Bora lá!
Escrevendo o Vetor Força
Digamos que uma força de módulo igual a esteja sendo aplicada em um ponto e a sua linha de ação percorre uma reta que passa por e por um outro ponto
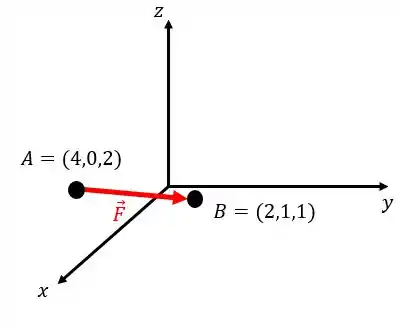
Nós sabemos que módulo da força é , mas não sabemos como escrevê-la na forma vetorial. Como vamos fazer isso?
Vamos escreve-la, da seguinte maneira, se liga!
Mas quem é esse ? Ele nada mais é do que o vetor normalizado que nos dá a direção dessa força. E como podemos encontra-lo?
Usando esses dois pontos!!! Os dois pontos definem uma direção, certo? E o sentido é a informação que diz que a força parte de para
Vamos montar o vetor que nos dará essa direção.
Mas não podemos esquecer de normalizar este vetor, ou seja, dividir cada um dos seus termos pelo módulo do vetor.
De uma forma geral, teríamos:
Para o nosso caso:
Ficou meio esquisito né? Que tal escrevermos com e ? Onde esses três vetores são os vetores unitários das direções e
Show de bola? Esse vetor define o sentido e a direção da nossa força.
Agora se quisermos escrever a força como um vetor, temos que multiplicar o seu módulo pelo vetor normalizado:
Onde é o módulo da força. Então vai ficar assim:
Esse vai ser basicamente o processo que vamos usar para escrever o vetor força. Faremos isso várias vezes nos exercícios.
Obs.: O vetor unitário é, em alguns casos, chamado de versor.
Projeções
Em forças , você aprendeu uma forma simples de se projetar uma força em uma direção qualquer. Agora vamos expandir nossos horizontes, afinal de contas, aumentamos uma dimensão nessa parada né?
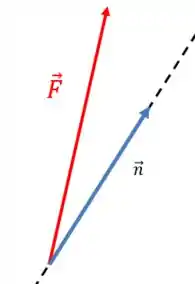
Mas não será tão complicado. Antigamente, você precisaria do ângulo entre a força e o vetor direção , certo? Agora não, pois para projetar a força na direção de qualquer, sendo um vetor unitário, basta você usar o produto escalar:
Então vamos fazer uma brincadeira? Que tal fazermos a projeção da força sobre o direção do exemplo anteior?
Pessoal, uma dica, o desenho abaixo está mostrando tanto a força quanto a direção . Mas não fique muito apegado ao desenho porque pode te confundir já que é um desenho tridimensional! Então olha rapidinho e parte para as contas, você vai ver que é mais simples!
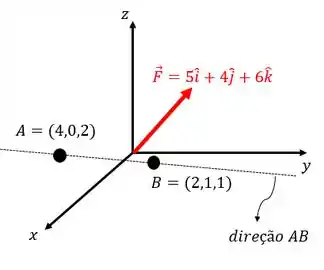
Aplicando a nossa equação vamos ter:
Substituindo (aqui vou usar a notação de parêntesis para ficar mais fácil de fazer o produto escalar):
Mas como vimos no tópico de vetores, isso aí em cima não gera um vetor, e sim um escalar. Então, para representar a projeção como um vetor, basta multiplicar o resultado acima por (afinal de contas, a projeção terá a direção do vetor unitário):
ou
Como a gente já tem vamos utilizar a segunda equação e obter:
Como temos um escalar multiplicando um vetor é só usar a distributiva:
Que pode ser escrito também como:
Ângulo entre Força e Eixo
Bom, você viu que não precisa saber o ângulo entre uma determinada direção e o vetor força para fazer a projeção. Mas e se você quiser saber este ângulo?
Basta você usar a outra forma do produto escalar:
Vamos fazer para o nosso exemplinho!! Lembrando que:
Qual será o ângulo entre a força e a direção de projeção?
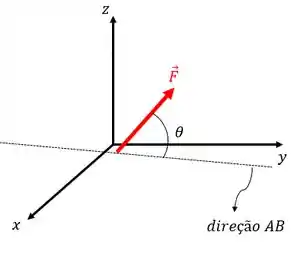
É só aplicar a equaçãozinha:
Agora precisamos do módulo de que será:
Show de bola achamos 1, isso porque esse vetor já é normalizado né? Contiuemos então. Agora precisamos achar o módulo de :
Como:
Então a gente pode substituir na equação:
obs: Pode não refletir muito bem na imagem porque estamos olhando um ângulo num sistema tridimensional beleza? Isso pode confundir mesmo!
De forma geral vamos ter o vetor normalizado então podemos fazer:
Se uma questão te pedir apenas o valor do ângulo que uma certa força faz com alguma direção, basta você utilizar qualquer vetor que esteja na mesma direção e no mesmo sentido da força.
Partiu fazer uns exercícios? 
Projeções
Ângulo entre Força e Eixo
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam& L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 53,2/99
Expresse vetorialmente em termos dos vetores unitários e. Determine o ângulo entre e o eixo
Passo 1
Vamos primeiro definir o vetor da direção Sendo o ponto
E o ponto
Temos:
Normalizando-o:
Passo 2
Agora é só definir a força usando o vetor:
Efetuando as contas, chegamos a isso:
Passo 3
Nesse caso, achar o ângulo que a força faz com o eixo é mais simples do que em outros casos que iremos ver. Basta você usar um triângulo retângulo:
Lembrando que o módulo de vale
Mas como a componente da força na direção do eixo y tem sinal negativo, devemos considerar o suplemento desse ângulo. Ou seja:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 53,2/103
A força de módulo e atua ao longo da diagonal do paralelepípedo, como mostrado. Expresse em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus componentes e
Passo 1
O sentido da força já está mostrado na figura.
Vamos definir o ponto inicial e final que definem o vetor direção da força:
Sendo esse o ponto extremo da face superior do paralelepípedo.
E:
Assim, o vetor direção será dado por:
E o vetor normalizado:
Passo 2
Assim:
Portanto,
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 53,2/100
A torre de transmissão de micro-ondas com de altura é equilibrada por três cabos de amarração, como mostrado. O cabo suporta uma força trativa de . Expresse em forma vetorial a força correspondente no ponto
Passo 1
Nós devemos descobrir quem é o vetor que vai do ponto inicial para o ponto
Esta é uma força trativa, pois ela tem uma tendência de fazer os dois pontos se aproximarem.
Passo 2
Beleza, então como vamos achar o vetor normalizado Vamos primeiro gerar o vetor:
é o ponto final e o inicial. Depois vamos normalizá-lo.
Pela figura, da pra perceber que:
E :
Então:
Assim, normalizando:
Então, a força será dada por:
Resposta
Exercício Resolvido #4
UFPE, P1, Giovanna, questão 1
Considere o sistema ilustrado na figura a seguir e determine os itens abaixo. (Use: e ).
- Calcule o versor na direção e defina a força em notação vetorial cartesiana em termos deste versor.
- Calcule a intensidade da componente de ao longo da direção
Passo 1
Vamos calcular primeiro o ângulo que a força faz com o plano
Então:
Assim:
Veja a figura de novo: se quisermos calcular a componente da força, primeiro temos que multiplicar por de modo a rebater a força para o plano e depois por para que ela fique no eixo .
Assim, a componente do versor é:
E a componente devemos multiplicar no final por
E a componente ? Apenas definida por:
E é negativa por que a força aponta para baixo!
E esse vetor já está normalizado? Sim e podemos comprovar isso calculando o seu módulo que deve dar como resposta:
Passo 2
Definindo a força em termos de
Passo 3
Basicamente, o item está te pedindo a projeção de em .
Pra isso, você tem que definir o vetor normal daquela direção. Então vamos trabalhar em cima do triângulo abaixo:
Perceba que a distância de até a origem é dada por:
Agora podemos calcular o ângulo que o versor faz com a horizontal:
Assim:
Então:
Passo 4
Agora é só fazer:
Resposta
Exercício Resolvido #5
UFPE, P1, Giovanna, questão 2
O tanque uniforme de é suspenso por meio de um cabo de de comprimento, que está preso às laterais do tanque e sobre a pequena polia localizada em Se o cabo pode ser preso nos pontos , determine qual amarração produz a menor quantidade de tração no cabo. Qual é esta tração?
Passo 1
Primeiramente, veja que a força precisa equilibrar o peso. Assim, o módulo dela vai ser sempre igual a:
Aqui nós vamos usar a regra do paralelogramo, visto em tópicos anteriores, pra calcular a tensão nos fios.
Como as distribuições em são sempre simétricas, a força será a mesma em ambos os cabos:
Então:
E o que vai mudar pra cada caso? O ângulo . Dessa forma, vamos conseguir analisar qual configuração gera o menor valor pra
Passo 2
Caso
O triângulo formado tem os seguintes ângulos:
Por que a hipotenusa dos triângulos retângulos tem
Porque o enunciado disse que o cabo tem de comprimento, assim, cada metade dele tem que ter
Com essas informações, podemos calcular
E
Show de bola, agora é fácil achar
Passo 3
Para o caso , vamos fazer a mesma coisa, só que as dimensões são outras:
E:
Assim, a amarração em produz a menor tensão e ela vale:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 53,2/104
O tensionador é apertado até que a força trativa no cabo valha Determine a expressão vetorial para a força trativa , como uma força atuando no elemento . Ache também o módulo da projeção de ao longo da linha
Passo 1
A força age no elemento , ou seja, no ponto Como a força é trativa, ela deve apontar de para .
Assim, o ponto é o ponto inicial e o final.
Podemos escrever a força trativa como:
Então, devemos achar esse vetor normalizado .
Passo 2
Pela figura do enunciado, o ponto é dado por:
E por:
Assim:
Assim:
Assim, a força pode ser escrita assim:
Passo 3
Pra gente achar a projeção da força em , primeiro temos que definir o vetor unitário que representa essa direção. Nós já sabemos quem é o ponto , precisamos só definir o ponto
Assim:
Então:
Passo 4
Para achar a projeção, basta fazer o produto escalar entre a força e o vetor que define a direção
Veja só: Com isso, nós achamos o módulo do vetor. E qual é a direção? A direção , claro. Então:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 54,2/110
Se está no centro da face do sólido retangular, expresse como um vetor em termos dos vetores unitários . Determina a projeção escalar de ao longo da linha . Os valores de e são conhecidos.
Passo 1
Vamos definir a direção . O ponto é o ponto inicial e origem do sistema, assim:
Já está no centro de uma das faces. Pela figura:
Assim:
E o vetor unitário nessa direção é dado por:
Passo 2
Assim, a força é definida por:
Passo 3
Para achar a projeção da força na linha , vamos primeiro definir o vetor unitário que simboliza essa direção:
Passo 4
Então, a projeção será dada pelo produto escalar abaixo:
Efetuando o produto termo a termo, vamos ter que:
E qual a direção? :
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 54,2/110
Determine o ângulo entre a força de e a linha
Passo 1
O ângulo é o mesmo ângulo que a direção faz com . Vamos procurar esse ângulo então:
Passo 2
A direção é dada por:
Passo 3
Agora, usando:
Então:
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 77,2/172
Uma força atua ao longo da linha dentro da casca cilíndrica circular, como mostrado. As quantidades são conhecidas. Usando as coordenadas mostradas, expresse como um vetor.
Passo 1
Essa é mais tranquila do que parece: primeiro vamos definir o vetor da direção
Depois, normalizando-o, vamos achar . Com esse vetor, vamos escrever a força como sendo:
Passo 2
O ponto pode ser definido por:
Dá pra ver pelo desenho?
No desenho não existe a sinalização de um ângulo e, além disso, o ponto está na face superior do cilindro. Assim, como o eixo é o eixo vertical, dá pra gente concluir que e as outras coordenadas são nulas.
E o ponto
Veja só: nesse caso, o raio faz um ângulo com a vertical. Além disso, ele está a uma distância da origem. Assim:
Passo 3
Então:
Bora calcular o vetor normalizado nessa direção, então?
Assim:
Passo 4
E por fim:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 55,2/116
Uma força é aplicada à superfície eda esfera como mostrado. Os ângulos localizam o ponto é o ponto médio de . Expresse de forma vetorial, usando as coordenadas dadas.
Dica:
Passo 1
Vamos primeiro analisar o plano , que faz um ângulo com :
Nós temos que achar quanto vale o ângulo , pois ele é o ângulo que a linha de ação da força faz com a horizontal, conforme o desenho acima.
Beleza, mas como achar isso?
Perceba que existe um triângulo retângulo que possui um dos ângulos como sendo . Nesse triângulo, os catetos são:
E esse adjacente tá certo? Sim, perca que a projeção de na horizontal é , porém a força parte do ponto , que o ponto médio do segmento . Esse segmento, por sua vez, tem o comprimento do raio da esfera.
Então:
Agora usando:
Arrumando isso e tirando raiz quadrada nos dois lados:
E usando:
Com isso, temos o que precisamos para calcular as componentes da força.
Assim, no segmento , a força tem como componente horizontal:
E vertical:
Passo 2
Beleza, mas essas componentes foram calculadas no segmento . Queremos saber as componentes nos eixos
Dá uma olhada:
Então, a componente é dada por:
E continua sendo o
Passo 3
Então, a força pode ser escrita como: