Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 111
Determine o ângulo entre a força de e a linha .
Passo 1
Primeiramente, vamos escrever em sua forma vetorial:
onde e é o vetor unitário que sai de em direção a , ou seja, na mesma direção e sentido de :
Passo 2
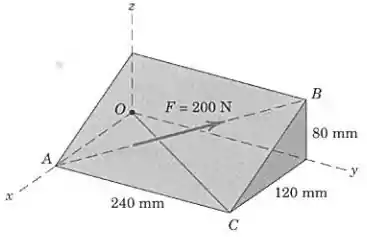
Conforme a figura do enunciado, o vetor é:
Então, podemos determinar o ângulo entre a força de e a linha por meio da seguinte fórmula:
Resposta
Exercícios de Livros Relacionados
Os cabos de tração são usados para suportar o poste telefônico. Represente a força em cada cabo na forma de um vetor cartesiano. Despreze o diâmetro do poste.
Dois cabos são usados para segurar a barra suspensa na posição e sustentar a carga de 1500N . Se a força resultante é direcionada ao longo da barra do ponto A para O , determine as intensidades da for
A porta é mantida aberta por duas correntes. Se as trações em A B e em C D são F A = 300N e F C = 250N , respectivamente, expresse cada uma dessas forças na forma de um vetor cartesiano.
Expresse a força F como um vetor cartesiano; depois determine seus ângulos de direção coordenados.
A torre é mantida no lugar pelos três cabos. As forças em cada cabo que atuam sobre a torre estão indicadas na figura. Determine a intensidade e os ângulos de direção coordenados α , β , γ da foça res