Binários e Resultantes
Teoria
Introdução
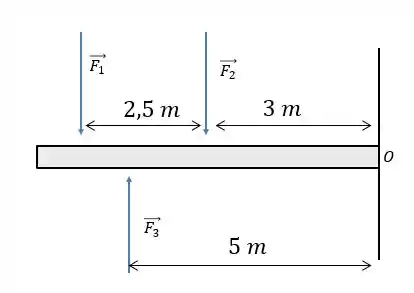
Imagine que temos uma barra, onde estejam atuando três forças assim:
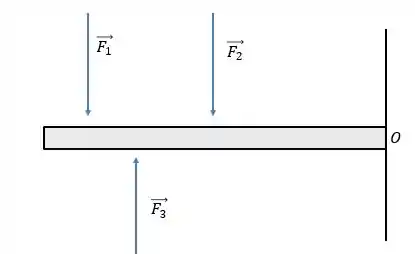
O que podemos fazer para facilitar a nossa vida? Podemos calcular a força resultante...
Vamos supor que após somar todas essas forças, a resultante ficou assim:
Mas onde esta força resultante vai estar localizada na peça?
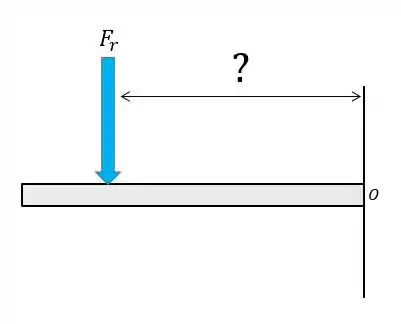
É isso que vamos aprender aqui. Partiu?
Sistema força-binário equivalente
Um binário é um conjunto de duas forças de mesmo módulo e direção, mas com sentidos contrários:
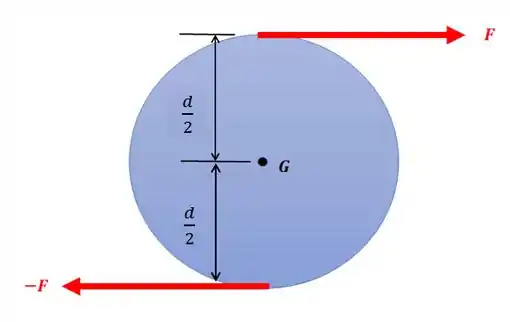
A soma das forças nesse corpo é nula:
Porém, a soma dos momentos não é nula. Olhando pra figura, ambas as forças estão a uma distância de do centro do círculo e isto acaba gerando um momento que podemos calcular assim (tomando como positivo o sentido horário):
Perceba que as duas forças fazem o círculo rodar em torno do seu centro no sentido horário. E isso que é o diferencial nos binários: eles fazem um corpo girar em somente um sentido.
O momento de um binário não depende do ponto de referência é sempre calculado pelo módulo de cada força multiplicado pela distância entre elas. Dizemos que o momento de um binário pode ser representado em qualquer posição do corpo, já que independe do ponto de referência.
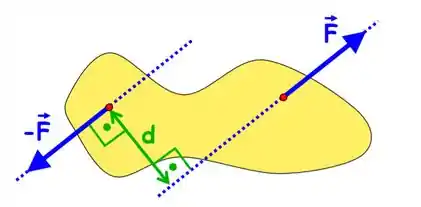
Essa propriedade vai nos permitir representar um sistema de forças por um sistema equivalente chamado de força-binário. Por exemplo, imagine que existe uma única força aplicada no ponto do corpo:
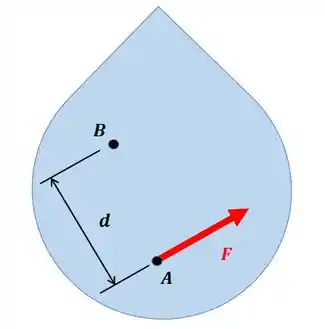
Como a gente faria para representar o efeito dessa força no ponto ? Essa força gera uma tendência no corpo de se mover na sua direção e também de girar. Então, para representar o efeito da força no ponto é só levarmos a força (mantendo seu sentido e direção) para o ponto e de quebra o momento que ela faz com relação a este ponto:
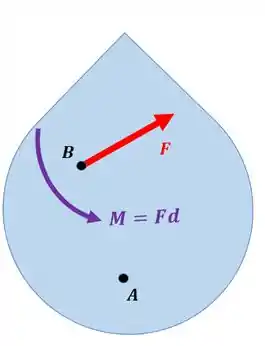
Essa representação nos diz que o corpo tende a girar em torno de e a se mover na direção do vetor . O momento é o binário do sistema força-binário equivalente.
Localização das Resultantes
Você já sabe achar a resultante de um conjunto de forças: basta somar todas elas, né?
Mas existe um problema: o que você acha nesse processo é o vetor força resultante, que indica uma direção e um sentido, maaaas você não sabe exatamente onde esta força está localizada.
Imagine que a barra abaixo sofre a ação de e :
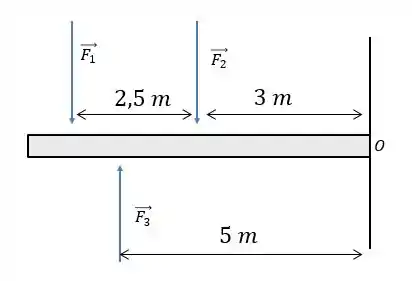
A resultante vai ser:
Mas onde ela vai estar localizada em relação ao ponto
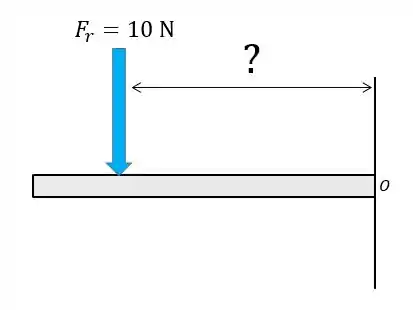
É isso que vamos aprender a fazer:
O primeiro passo é calcular o momento resultante em relação ao ponto , ou seja, o somatório de todos os momentos:
Então vem o pulo do gato: O momento exercido pela força resultante é igual ao momento resultante. Ou seja:
Com isso, você consegue achar o
Simples né? Então, o que você deve fazer é:
- Calcular a força e o momento resultante em relação a algum ponto, o que equivale a achar o sistema força-binário equivalente.
- Usar a relação momento causado pela força resultante e momento resultante abaixo:
Com isso, você consegue achar e localizar a força resultante.
O somatório dos momentos das forças inciais era:
Lembre-se que vamos considerar o sentido anti-horário positivo:
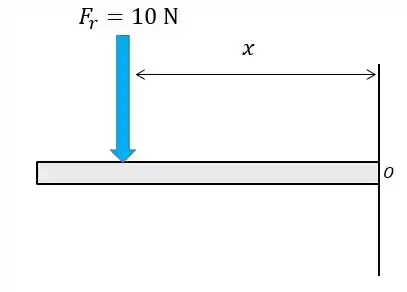
Agora é só igualar ao momentod a força resultante:
Bora praticar? 
Sistema força-binário equivalente
Localização das Resultantes
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 40,2/57
O conjunto roda/suporte está submetido ao par de forças de mostrado. Determine o momento associado a essas forças.
Passo 1
Primeira coisa: as forças são iguais, certo? Além disso, eles tendem a girar a roda no mesmo sentido, certo?
Então, temos um binário cujo momento será dado multiplicando o módulo da força pela distância entre elas:
Não acredita em mim? Podemos calcular o momento da maneira tradicional, ou seja, multiplicando cada força pela sua respectiva distância até o ponto :
Beleza! Se a gente adotar como positivo rotações no sentido anti-horário, então teremos
Isso por que essas forças tendem a fazer a roda girar no sentido horário!
Se quiséssemos escolher como positivo rotações no sentido horário, então teríamos positivo 😉
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 41,2/65
Uma chave de roda é usada para apertar um parafuso de cabeça quadrada. Se forças de forem aplicadas a chave, como mostrado, determine o módulo das forças iguais exercidas nos quatro pontos de contato na cabeça de do parafuso, de modo que seu efeito externo sobre o parafuso seja equivalente ao das duas forças de Considere que as duas forças são perpendiculares aos lados planos da cabeça do parafuso.
Passo 1
O sistema de forças inicial é esse aqui:
Não importa muito o sinal do momento. Queremos apenas saber depois quais forças vão gerar um torque equivalente a esse.
Assim, o momento, em módulo, pode ser calculado por:
Notou que multiplicamos por dois pois as duas forças giram a peça no mesmo sentido, né?
Passo 2
Agora o nosso sistema é esse aqui:
Beleza? Não sabemos o módulo de , mas sabemos que ela produz o mesmo torque que antes. Assim:
Resposta
Exercício Resolvido #3
P1, Estácio
A chave é usada pra soltar um parafuso, conforme a figura abaixo. Determine o momento de cada força sobre o eixo do parafuso passando pelo ponto
Passo 1
Perceba que se formos usarmos o teorema de Varignon, o momento da componente da força vai ser nulo, pra ambas as forças.
Por quê? Dá uma olhad ano desenho: a linha de ação dessas forças passa pelo centro :
Show? Então, facilitando a nossa vida, vamos apenas calcular as componentes verticais e multiplicar pelas distâncias ao ponto .
Passo 2
Assim:
Perceba que na segunda força usamos o seno.
Como a questão não tá pedindo os sinais dos momentos, vamos apenas calcular os módulos:
Assim, a resposta é a letra
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 41,2/66
Durante uma curva suave para a direita, uma pessoa exerce as forças mostradas sobre o volante. Observe que cada força consiste em uma componente tangencial e em uma componente radial direcionada para dentro. Determine o momento exercido em relação à coluna de volante
Passo 1
Nós apenas precisamos lidar com o ângulo de , afinal de contas, ele é o ângulo que a força faz com a tangente ao círculo. A partir dele, vamos decompor a força em um vetor na direção do raio (radial) e que não realiza momento, e uma componente tangencial que realiza o momento.
Passo 2
A linha pontilhada representa a direção tangencial ao círculo:
Assim, podemos perceber que a componente tangencial é dada por:
E a radial:
A componente na direção radial não realiza momento, então:
Perceba que somamos os momentos das duas forças, pois eles tem o mesmo sinal.
Então:
Resposta
Exercício Resolvido #5
FASETAC, Lista 8
O tubo está fixo em Substituir as duas forças aplicadas por um sistema força-binário na seção
Passo 1
Pra achar a força resultante, vamos considerar como sentido positivo de o que foi indicado na figura. Assim, a força resultante é:
Passo 2
Ambas as forças tendem a girar a barra no mesmo sentido, no caso, o sentido horário. Assim, podemos dizer que o momento resultante vale:
O sinal é esse mesmo? Não, pela regra da mão direita, a rotação nesse sentido vai gerar um vetor na direção contrária ao eixo
Passo 3
Podemos representar o sistema força-binário resultante por:
Resposta
Exercício Resolvido #6
FASETAC, lista 8
Três forças horizontais , e são aplicadas, como ilustrado, a um suporte vertical de ferro fundido. Substitua as três forças e por um sistema força-binário na seção que contém o ponto
Passo 1
Primeiramente, vamos calcular a força resultante do sistema. Tomando o sentido de e como o positivo, podemos dizer que:
Passo 2
Agora vamos calcular o momento resultante. Considerando o sentido anti-horário como o positivo, percebemos que e exercem momentos positivos, já exerce um momento negativo. Podemos dizer então que:
Perceba que não contabilizamos a distância de , já que o ponto que estamos analisando é o ponto que está a da base.
Passo 3
Assim, o sistema pode ser representado por:
Resposta
Exercício Resolvido #7
FASETAC, lista 8
Duas forças são aplicadas de são aplicadas, como ilustrado, aos vértices e de uma placa quadrada de de lado. Determine o momento do binário formado pelas duas forças.
Passo 1
Primeiro perceba que as forças têm módulos iguais, mas sentidos contrários. Assim, a força resultante é nula:
Passo 2
Bora calcular o momento agora. Vamos decompor cada uma das forças em uma componente tangencial e uma perpendicular. As forças tangenciais realizarão um trabalho de sinal igual ao das forças normais. Veja na figura abaixo:
Passo 3
Assim, o momento pode ser dado por:
Resposta
Exercício Resolvido #8
FASETAC, lista 8
Quatro pinos de de diâmetro são presos a uma tábua. Dois barbantes, apoiados nos pinos são tracionados, como ilustrado.
Determine o binário resultante na tábua.
Se apenas um barbante é usado, em quais pinos deverá ser apoiado e em que direções deverão ser tracionados a fim de que se produza o mesmo binário com uma força de tração mínima?
Qual o valor dessa força de tração mínima?
Passo 1
A resultante das forças é zero, afinal de contas, existem forças de mesmo módulo e sentidos contrários.
Em relação ao momento resultante, perceba que existem dois pares de forças que são igualmente espaçadas do centro da placa. Repare que a distância do ponto de aplicação da força até o centro do parafuso deve considerar o raio do parafuso. 25662
Assim, podemos calcular o momento resultante por:
Esse será o nosso momento do binário resultante:
Passo 2
Podemos apoiar em ou:
Os sentidos das tensões devem ser sempre contrários.
Passo 3
No caso de , a distância entre as forças vale . Assim:
Ou seja, o par de forças precisa exercer o mesmo momento que o binário, por isso a igualdade acima.
E no caso :
Assim, a tensão mínima vale e é gerada na configuração
Resposta
Exercício Resolvido #9
FASETAC, lista 8
Um momento de é aplicado pela mão do operário. Determine o binário de forças , que age na mão do operário e que atua na ponta da chave da fenda.
Passo 1
Já temos o binário equivalente e, nesse sistema força-binário, claramente a resultante das forças é zero, já que as forças apontam em sentidos contrários e tem o mesmo módulo.
Para o caso , temos que a distância entre as forças vale , assim:
Passo 2
E no caso de ,
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 42,2/72
O suporte está preso a uma coluna por meio de dois rebites, e, e suporta uma força de . Substitua essa força por uma força atuando ao longo da mediatriz dos rebites e por um binário. Em seguida, redistribua essa força e o binário, substituindo-os por duas forças, uma em e outra em , e determine as forças suportadas pelos rebites.
Passo 1
Para representar o sistema por um sistema força-binário, temos que calcular primeiro o momento que a força faz na mediatriz de .
Pra isso, temos que usar a distância entre o ponto de aplicação da força e a mediatriz de
O momento é dado por:
Passo 2
Assim, o sistema binário-resultante é dado por:
Passo 3
Pra redistribuir a força e o binário, primeiro vamos calcular o par de forças que sozinhas gerariam o momento desse binário:
Quem é essa distância? É a distância de cada parafuso até a mediatriz:
Entendeu o motivo de ser Ambas as forças giram no mesmo sentido:
Passo 4
Já lidamos com o momento, agora precisamos lidar com a resultante das forças. Sabendo que ela vale , podemos dizer que em cada parafuso agem
Passo 5
Agora precisamos fazer a superposição dessas duas situações. Como? Somando as forças:
De acordo com os sentidos, teremos:
Resposta
Exercício Resolvido #11
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 41,2/67
A força de está aplicada do corpo Se , determine o sistema força-binário equivalente no eixo, em
Passo 1
Se a força faz com o eixo e faz com o eixo , podemos dizer que faz com o eixo
Na verdade, , mas podemos considerar esse efeito na componente da força, que será negativa:
A componente da força também será negativa porque aponta para esquerda.
Esse será o mesmo vetor força resultante que atuará em . Vamos descobrir o momento total agora.
Passo 2
Sabendo o ângulo que faz com o eixo , vamos calcular os momentos, como fizemos antes, calculando o momento causado por e as projeções horizontais das distâncias e por e as projeções verticais das distâncias.
No primeiro caso, teremos o seguinte esquema:
Assim, considerando o sentido anti-horário como positivo:
Passo 3
E o sistema :
Assim:
Passo 4
Assim, o momento total será a soma dos dois:
A representação do sistema equivalente força-binário é:
Resposta
Exercício Resolvido #12
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 42,2/72
As rodas do automóvel de tração dianteira sofrem, em conjunto, a ação de uma força de reação normal de e de uma força de fricção , ambas exercidas pela superfície da estrada. Se é sabido que a resultante destas forças faz um ângulo de com a vertical, determine o sistema força-binário equivalente no centro de massa do carro. Trate esse problema como sendo bidimensional.
Passo 1
A força resultante faz um ângulo de com a vertical:
Nós sabemos quem é , mas não sabemos quem é . Porém, podemos usar:
Passo 2
Assim, o módulo da força resultante vale:
E a força resultante pode ser escrita como:
Passo 3
Agora precisamos calcular o momento resultante. Para isso, vamos usar as componentes separadamente:
A componente friccional está a de , então:
E a componente normal está a de
Ambas as forças fazem o corpo girar no mesmo sentido, então:
Assim, o sistema equivalente força-binário em tem as seguintes características:
Resposta
Exercício Resolvido #13
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 48,2/93
Duas polias estão submetidas às forças trativas das correias, como mostrado. Se a resultante destas forças passa pelo centro , determine , o módulo de e o ângulo anti-horário que faz com o eixo
Passo 1
Quando a questão nos diz que a resultante das forças passa em um ponto, também está dizendo que o momento resultante naquele ponto é nulo.
Faz sentido né? Afinal de contas, se a combinação de todas as forças produz uma força que não exerce momento em certo ponto, é natural pensar que o momento resultante ali é nulo.
Então, o que sabemos é que:
Passo 2
Assim, vamos calcular o momento que cada força exerce em relação ao ponto , somar tudo e igualar a zero (tomando o sentido horário como o positivo):
Show? Encontramos parte de nossa resposta.
Passo 3
Agora, de posse do módulo de , podemos calcular a resultante . Mas antes, vamos escrever cada força em termos de vetores e
- As forças de e
- e
Assim, é dado por:
Assim, o módulo de é dado por:
Passo 4
Falta a gente descobrir qual é o ângulo que faz com o eixo . Por enquanto, o que sabemos é que a resultante se localiza no primeiro quadrante, já que a componente horizontal e a vertical são positivas:
Podemos, então, calcular a tangente desse ângulo
Resposta
Exercício Resolvido #14
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 48,2/88
As direções dos dois vetores de empuxo de um avião experimental podem ser variadas independentemente, dentro de certos limites, desde a direção convencional à frente. Para a configuração de empuxo mostrada, determine o sistema força-binário equivalente no ponto Substitua, então, este sistema força-binário por uma única força e especifique sobre o eixo pela qual passa a linha de ação da resultante. Estes resultados são vitais para analisar o desempenho do projeto.
Passo 1
Para determinar o sistema equivalente força-binário, vamos calcular a força resultante e o momento resultante em relação ao ponto
Perceba que a força do propulsor de tem um braço de alavanca de , assim como a componente horizontal da força do propulsor de . Já a componente vertical da força de está distante do ponto . Adotando o sentido horário como o positivo, temos que:
Com a força e o momento, temos o sistema força-binário equivalente em
Passo 2
Vamos considerar que a barra abaixo representa o nosso avião. Quando calculamos o sistema força-binário equivalente no ponto , a configuração fica assim:
Ou seja, a força e o momento resultante ficam localizados em que é o nosso ponto de referência.
Agora queremos deslocar a força resultante ao longo de para que ela gere o mesmo momento que o binário gera.
Olhando para a figura, sabemos que ela precisa andar na direção negativa de (considerando que em , porque assim o momento terá sentido horário:
Além disso, apenas a componente em da força resultante () realizará momento, pois só ela terá um braço de alavanca.
Passo 3
Assim, podemos dizer que:
Por que o sinal de menos? Apenas para no final da conta ter um negativo. Ele precisa ser negativo, como vimos. Então:
Pronto!
Resposta
Exercício Resolvido #15
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 48,2/96
A roda traseira de um automóvel de tração dianteira que está acelerando para a direita está submetida às cinco forças e ao momento mostrado. As forças e são forças transmitidas pelo eixo à roda, é a força de fricção exercida pela superfície da estrada no pneu, éa força normal de reação exercida pela superfície da estrada e é o peso do conjunto pneu/roda. O momento é devido à fricção do mancal. Determine e localize a resultante do sistema.
Passo 1
Primeiro vamos calcular a resultante das forças. Para isso, vamos antes escrever cada força em termos de e (veja na figura as forças que são totalmente verticais ou horizontais):
Passo 2
Assim, a resultante é dada por:
Ou seja, a nossa resultante é totalmente horizontal. Vamos agora calcular o momento resultante total do sistema e depois a localização da resultante das forças.
Passo 3
Vamos calcular o momento total em relação ao ponto .
Isso vai nos ajudar porque apenas a força exerce momento nesse ponto. Veja na figura: As outras forças têm linhas de ação que cruzam com
Assim, o sistema pode ser simplificado para:
Tomando o sentido horário como positivo, teremos:
Passo 4
Show de bola. Agora só precisamos descobrir a localização da resultante.
Podemos tirar uma informação importante do nosso momento resultante e do sentido da força resultante.
O momento resultante é no sentido horário e a força resultante aponta no sentido positivo de . Assim, considerando como referência, a força resultante vai estar localizada acima desse ponto:
Pra descobrir quanto vale , basta usarmos:
Então, a resultante está acima do ponto .
Resposta
A resultante está acima do ponto .