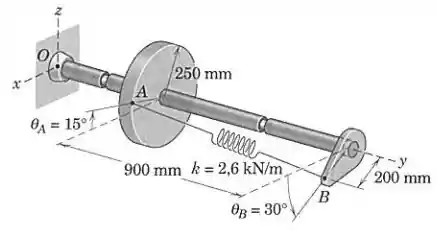
A mola com constante está presa ao disco no ponto e à placa da extremidade no ponto , como mostrado. A mola não está esticada quando e são, ambos, zero. Se o disco é girado no sentido horário e a placa é girada de no sentido anti-horário, determine uma expressão vetorial para a força que a mola exerce no ponto . O módulo da força da mola é a constante multiplicada pela deflexão (alongamento ou encurtamento) da mola.

O comprimento da mola não esticada deve ser:

E o comprimento da mola esticada é a distância :

Portanto, a deflexão da mola será:

Sabendo que , obtemos o módulo da força da mola:

Finalmente, podemos expressar a força vetorialmente: