Carga crítica e análise para diversos tipos de apoio
Produzido por Pablo RicardoTeoria
E aí, abiguinhos!! Como vocês estão? Espero que estejam muitíssimo bem!!!
Hoje vamos falar um pouco mais sobre a carga crítica. A gente já viu que a carga crítica para uma coluna apoiada em pinos, ou qualquer outra forma que possibilite uma angulação é dada por:
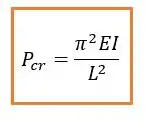
Onde:
- é o comprimento
- o coeficiente de elasticidade
- que é o momento de inércia.
Equação geral da carga crítica
Beleza, mas e se a nossa coluna tiver um apoio que não permite rotação?
Antes a gente tinha a equação como:
Onde o termo era o momento interno da coluna.
Agora a gente tem que ir adicionar um termo referente ao momento do apoio também:
Ou seja, adicionamos um termo relativo ao momento imposto pelo apoio que impede a rotação.
Aí é só resolver essa equação diferencial aí...

Você não precisa resolver essa equação não pô! Sabe por quê? Porque alguém já fez isso pra gente e pra falar a verdade a solução ficaria MUITO parecida com a solução do primeiro caso (do apoio como um pino). Fica assim:
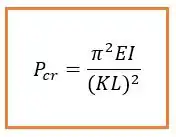
Viu que a única diferença é o termo ? Esse termo é chamado de fator de comprimento efetivo, e o termo é o comprimento efetivo .
Comprimento efetivo
Pessoal, comprimento efetivo é o comprimento que vamos utilizar no lugar do comprimento normal na equação, e esse comprimento varia de acordo com cada tipo de apoio.
Por exemplo, se pegarmos um apoio do tipo em pinos o nosso fator de comprimento efetivo vai ser igual 1. Aí a gente volta para a equação lá do começo, faz sentido né?
Podemos escrever a nossa equação então em função do comprimento efetivo:
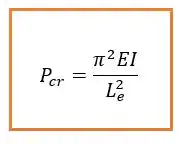
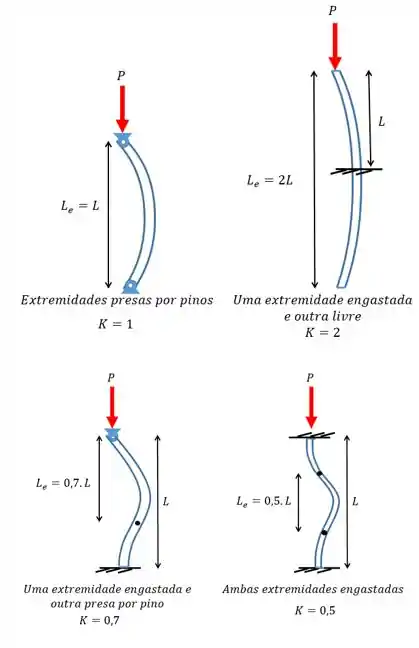
E se for outro tipo de apoio a gente tem que olhar o esqueminha aqui embaixo:
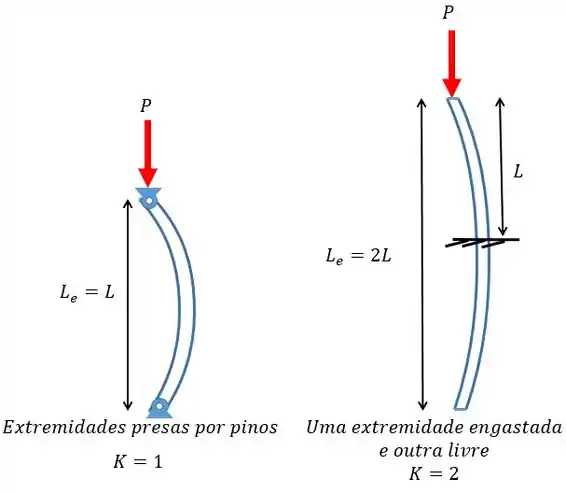
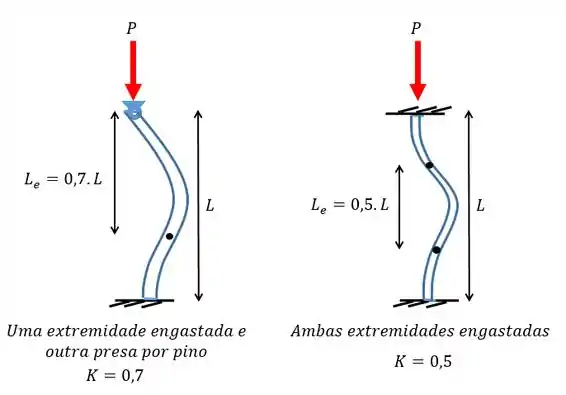
Aí é só ver qual o apoio e substituir o valor de para achar na fórmula!
Perceba que dependendo da configuração a carga crítica pode aumentar ou diminuir, dependendo do valor de .
Tensão crítica
Pessoal, a gente também pode definir a tensão crítica para diversos apoios também. Só lembrar que:
Substituindo na equação vamos obter:
Agora a gente ainda pode utilizar mais um macete! O momento de inércia pode ser dado como a área vezes o raio de giração ao quadrado, lembram disso?
Sendo assim a gente pode substituir na equação e obter:
Simplificando o termo da área:
Essa equação muitas vezes é escrita da forma:
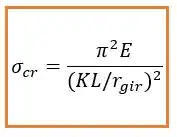
Mas não faz diferença nenhuma! É a mesma coisa só com uma carinha diferente. O legal é que o termo é definido como índice de esbeltez efetivo.
Agora vamos resolver uns exercícios!!!
Comprimento efetivo
Tensão crítica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Dadas as colunas abaixo, todas sujeitas aos mesmos carregamentos, com as mesmas dimensões e feitas do mesmo material. Qual delas é a que melhor resiste à flambagem? E qual é a que pior resiste?
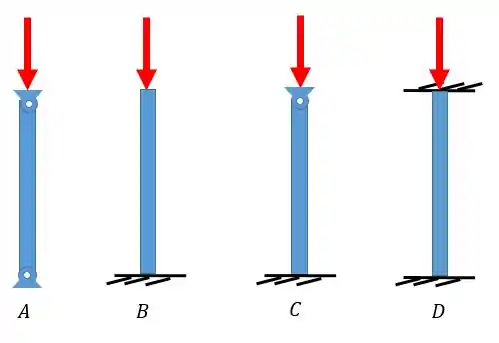
Passo 1
Fala aí, galerinha!! Bom essa questão diz basicamente que tudo é idêntico em cada barra, exceto é claro os apoios. A gente já estudou que apoios diferentes causam reações diferentes na reação da flambagem, modificando o comprimento efetivo da barra.
Lembre-se que a nossa carga crítica pode ser escrita como:
Dessa forma quem possuir o menor comprimento efetivo, possuirá a maior resistência à flambagem.
Passo 2
Show de bola! Mas quem tem o maior comprimento efetivo?
Se a gente lembrar que o comprimento efetivo é igual ao produto do fator de comprimento efetivo vezes o comprimeno da barra . Então a gente pode notar que queremos o menor .
Para achar o menor é só olhar na nossa tabelinha:
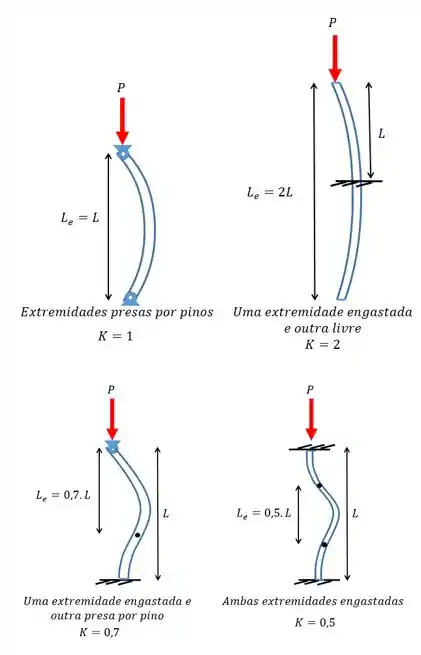
Viram que o tipo de engaste que fornece o menor é o que possui ambas as extremidades engastadas?
Então esse é o mais resistente à flambagem, resposta letra . Já o pior é um lado engastado e outro livre
Passo 3
Então esse é o mais resistente à flambagem, resposta letra . Já o pior é um lado engastado e outro livre
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
A figura a seguir mostra uma coluna de aço feita com perfil . Sabendo que a coluna está engastada na base e presa por um pino no topo calcule a maior força que pode ser aplicada sobre a coluna para que ela não sofra flambagem.
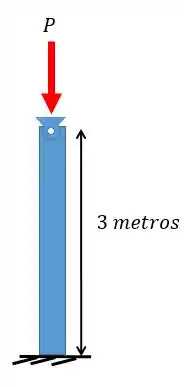
Passo 1
Pessoal, o problema quer que achemos a maior carga possível, ou seja, a carga crítica de flambagem que é dada pela equação:
Como nós temos o perfil podemos achar o momente de inércia por meio da tabela de perfis de abas largas, o módulo de elasticidade foi dado, o coprimento também foi dado.
Falta apenas o fator que podemos achar pela tabela de tipos de apoio. Então partiu resolver.
Passo 2
Vamos começar com o momento de inércia. Como temos um perfil então temos:
Esse valor pode ser achado em tabelas de perfil de abas largas em qualquer livro de resistência dos materiais =D
Só fique atento porque a tabela fornece valores do momento de inércia em ambos os eixos. Nós devemos escolher o momento de inércia com menor valor, pois aí onde vai acontecer a flambagem.
Passo 3
Agora vamos achar o fator de comprimento efetivo . Podemos ir lá na teoria e achar o seguinte:
Como se trata de uma extremidade engastada e outra presa por pino vamos ter:
Passo 4
Agora é só substituir na equação:
Pessoal, aqui é importante notar que esse valor provavelmente irá ultrapassar os limites de escoamento do aço, devido à pequena área da seção transversal do perfil. Mas como o problema não pediu para fazermos essas análise vamos manter essa resposta.
Passo 5
Pessoal, aqui é importante notar que esse valor provavelmente irá ultrapassar os limites de escoamento do aço, devido à pequena área da seção transversal do perfil. Mas como o problema não pediu para fazermos essas análise vamos manter essa resposta.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração própria
Dois estudantes de engenharia, depois de tomar algumas cervejas, decidem entrar na faculdade e realizar um teste de flambagem utilizando uma máquina de compressão. Sabendo que os dois alunos utilizaram um corpo de prova de aço com de comprimento e de seção retangular com , sabendo também que eles posicioram o corpo de prova de forma que esteja engastado em ambos as extremidades, diga se eles conseguirão chegar ao ponto de flamgabem ou se o material irá escoar antes.
Passo 1
Que questão doida essa né? kkkk
Enfim, vamos ao que importa. A questão pede para avaliarmos o que acontece primeiro a flambagem ou o escoamento. Para isso a gente vai precisar calcular a tensão crítica de flambagem e comparar com a tensão de escoamento. Faz sentido não faz?
Só para lembrar que o problema deu a tensão de escoamento e a tensão crítica de flambagem pode ser encontrada através da seguinte equação:
Ou
obs: É a mesma equação. A única diferença é a consideração do raio de giração
Passo 2
Bom, partiu então resolver. Vamos calcular a tensão crítica de flambagem, para isso temos que calcular o momento de inércia e área.
Área:
O momento de inércia:
Como o momento de inércia deve ser o menor possível relativo à seção transversal vamos ter:
Só precisamos de mais uma coisinha antes de substituir na equação da tensão crítica, é saber qual o valor do fator de comprimento efetivo . Pela tabela nós vamos ter que para o caso de ambas as extremidades engastadas
Passo 3
Agora sim é só substituir na equação:
Percebe que esse valor é bem superior ao valor da tensão máxima de escoamento
Logo, os nossos dois estudantes alcoolizados não conseguiram realizar o teste de flabagem, pois o corpo de prova falhou devido à compressão antes.
Passo 4
Percebe que esse valor é bem superior ao valor da tensão máxima de escoamento
Logo, os nossos dois estudantes alcoolizados não conseguiram realizar o teste de flabagem, pois o corpo de prova falhou devido à compressão antes.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Uma coluna de aço tem 10 metros de comprimento e é engastada em ambas extremidades, essa coluna utiliza um perfil . Como o momento de inércia de um dos eixos do perfil é bem menor do que o outro um reforço foi adicionado, além disso podemos considerar que o reforço está engastado na coluna. Qual a carga crítica suportada pela coluna de forma a não ocorrer flambagem?
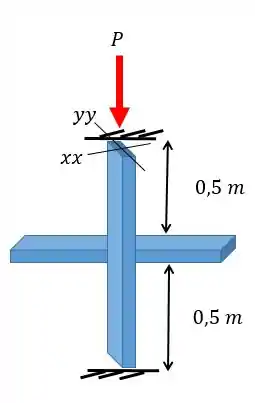
Passo 1
Faaala, galera! Nesse problema a questão pede a máxima carga que pode ser aplicada ao nosso sistema, então precisamos basicamente aplicar a equação da carga crítica:
A gente só precisa prestar atenção com o fato de existir o tal do reforço. Por causa do reforço, a flambagem vai ocorrer diferentemente em cada eixo. Olha só no próximo passo como isso vai acontecer.
obs: O importante é perceber que o reforço segmenta a coluna e isso reduz o comprimento efetivo, o que por sua vez aumenta a carga crítica.
Passo 2
Vamos começar olhando os momentos de inércia do perfil , que são tabelados segunda a tabela “perfis de abas largas”:
A gente pode perceber que o momento de inércia do eixo é bem superior ao do eixo . Por esse motivo o reforço é utilizado para a flambagem no eixo , não é necessário que se utilize o reforço no eixo .
Sendo assim o eixo vai suportar a flambagem normalmente com ambas as extremidades engastadas. Vamos ter:
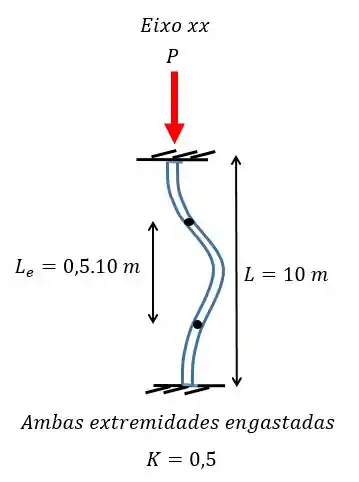
E podemos achar o valor da carga crítica
Passo 3
Agora vamos partir para a flambagem no eixo . Neste caso, por causa do reforço, a coluna irá atuar como duas colunas uma em cima da outra. Dessa forma o comprimento que devemos utilizar é apenas a metade. Como o reforço está engastado na coluna vamos ter algo do tipo:
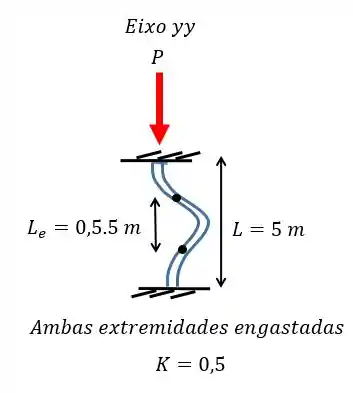
E podemos aplicar a equação normalmente:
Perceba que mesmo com o reforço a carga máxima suportada no eixo é inferior ao do eixo .
Logo a máxima carga para que não ocorra flambagem é de .
Passo 4
A máxima carga para que não ocorra flambagem é de .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
Uma coluna de aço com perfil é utilizada para suportar uma carga como mostra a figura. Sabendo que a base esta engastada e o topo com duas cordas impedindo a movimentação na direção . Qual a carga crítica suportada pela coluna de forma a não ocorrer flambagem?
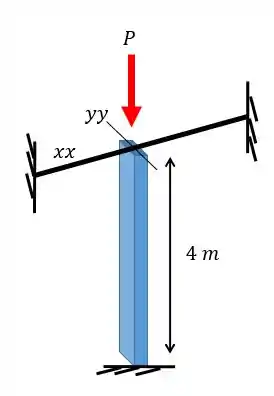
Passo 1
Galerinha, o ponto crucial dessa questão é entender que a corda impede a movimentação do topo apenas no eixo . Dessa forma vamos ter dois casos de flambagem:
- Eixo – Flambagem com uma extremidade engastada e a outra, que é a das cordas, pode ser considerada apoiada em pinos. Isso acontece porque o movimento de translação é impedido mas o topo ainda é livre para rotacionar.
- Eixo – Onde a corda não faz efeito, sendo assim, teremos uma extremidade engastada e a outra solta.
Aí é só fazer o cálculo separadamente e utilizar a menor carga. É legal a gente ver que essas diferenças de apoios irão influenciar diretamente no comprimento efetivo que é dado por
Passo 2
Vamos começar pelo eixo . A primeira coisa que vamos fazer é ir na tabela de perfis de abas largas e achar o momento de inércia do perfil .
Depois a gente tem que lembrar que no caso de uma extremidade engastada e outra apoiada em pinos vamos ter:
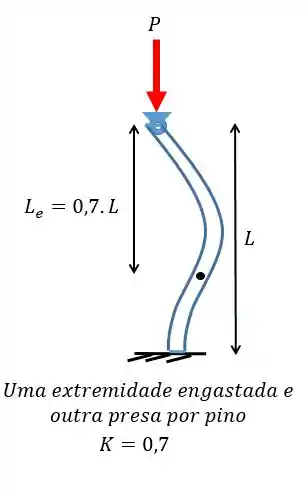
Dessa forma podemos substituir na equação da flambagem
Passo 3
Agora vamos fazer para o eixo . Na mesma tabela vamos achar o momento de inércia em relação ao eixo :
Depois a gente tem que lembrar que no caso de uma extremidade engastada e outra livre vamos ter:
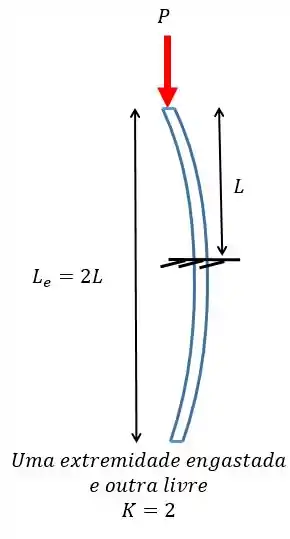
Dessa forma podemos substituir na equação da flambagem
Logo a carga crítica é a menor de ambas e será dada por
Passo 4
Logo a carga crítica é a menor de ambas e será dada por
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.4
Uma coluna de aço tem comprimento de e está engastada na base e presa por pinos no topo. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica.
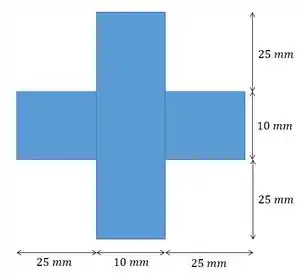
Passo 1
Olá, meus miguxos!
Essa questão aqui você talvez já até tenha feito uma parecida mas agora temos um ponto que fazer toda a diferença!
O problema nos diz que a coluna está engastada na base e presa por pinos no topo, a equação da carga crítica é:
E vai ser exatamente essa carga crítica que o problema vai querer!
O problema nos disse que é um aço , que tem , e também forneceu o comprimento da coluna de . Então para achar a carga crítica a gente precisa calcular o momento de inércia e descobrir quanto vale esse termo e substituir na equação!
Passo 2
Primeiro vamos achar o termo . Esse termo é definido unicamente pelas condições dos apoios e segue sempre o mesmo padrão, e a gente viu na teoria que para o caso engastado na base e topo preso por pino vamos ter :
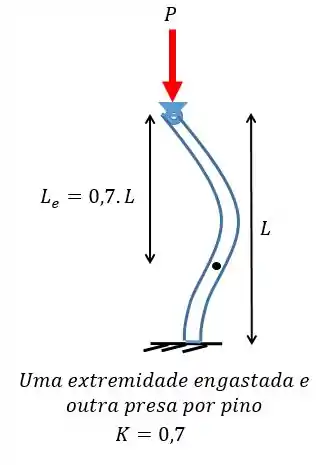
Pronto! Agora é só calcular o momento de inércia e partir pro abraço!
Passo 3
Como a seção é simétrica então não precisamos nos preocupar com qual eixo vamos analisar porque:
Agora para calcular a gente tem uma figura composta por duas barras, então vamos calcular cada barra separadamente e somar os momentos resultantes:
Aí aqui não tem muito segredo, a base de uma é igual a altura da outra, logo:
E
Passo 4
Agora é só substituir na equação da força crítica:
Passo 5
Pessoal, a gente já até achou a carga crítica mas é importante também saber se não ultrapassamos o limite de escoamento do material também. Como o aço tem , então a gente vai fazer:
A área da seção eu vou calcular como um quadradão () menos 4 quadradinhos :
Então vamos ter:
Como essa tensão é menor do que então a nossa coluna pode ser utilizada no projeto já que não irá flambar e nem escoar =D
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.9 (adaptado)
Uma coluna de aço tem comprimento de e está engastada na base e livre no topo. Se a área da seção transversal river as dimensões mostradas na figura, determine a carga crítica
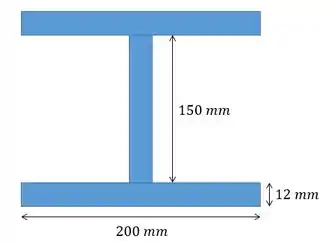
Passo 1
Bom dia, pessoal!!!
Olhem só como essa questão foi boa com a gente rsrs...
Ela já falou que o aço será utilizado, logo e . Além disso forneceu o comprimento . Se a gente olhar nossa equação da carga crítica vamos ter:
Então falta só a gente calcular o momento de inércia e achar o valor de . Então partiu achar essas coisitchas.
Passo 2
Primeiro vamos achar o termo . Esse termo é definido unicamente pelas condições dos apoios e segue sempre o mesmo padrão, e a gente viu na teoria que para o caso engastado na base e livre no topo vamos ter :
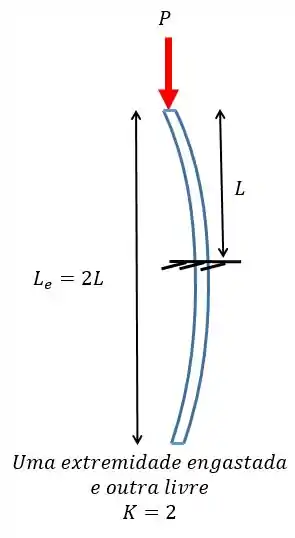
Pronto! Agora é só calcular o momento de inércia e partir pro abraço!
Passo 3
Pessoal, a flambagem sempre vai ocorrer no eixo de menor momento de inércia, correto? Correto! Isso tem que ter no sangue!!!
Como temos um perfil de abas largas é importante saber que o eixo de menor momento de inércia é o aquele que passa exatamente pela alma:
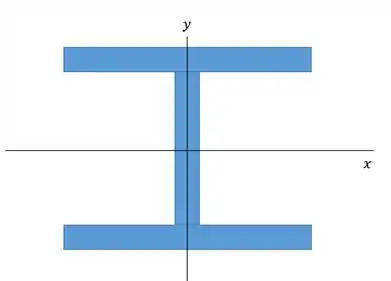
Então o nosso momento de inércia será calculado como a soma de cada uma das três barras, utilizando o eixo como a base:
Passo 4
Agora é só substituir na equação da força crítica:
Passo 5
Pessoal, a gente já até achou a carga crítica mas é importante também saber se não ultrapassamos o limite de escoamento do material também. Como o aço tem , então a gente vai fazer:
Calculando a área vamos ter:
Então vamos ter:
Como essa tensão é menor do que então a nossa coluna pode ser utilizada no projeto já que não irá flambar e nem escoar =D
Resposta
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 487. Problema 13.11
O elemento estrutural é feito de aço e usado como uma coluna de de comprimento. Se as extremidades da coluna estiverem engastadas, a coluna pode suportar a carga crítica sem escoamento?
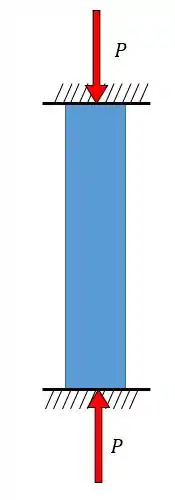
Passo 1
Falaaa, galerinha!!! Olha essa questão que interessante!! O problema já nos traz o fato de que não podemos analisar apenas a questão da flambagem. Isso porque algumas vezes a nossa coluna resiste à flambagem mas escoa por compressão e isso é muito ruim! Isso acontece quando temos uma coluna muito grossa, pouca esbelta.
Mas voltando ao problema, vamos fazer o basicão: calcular a força crítica e depois ver se essa força gera uma tensão maior ou menor do que a tensão de escoamento do aço.
A questão já falou que o aço será utilizado, logo e . Além disso forneceu o comprimento . Se a gente olhar nossa equação da carga crítica vamos ter:
Então falta só a gente calcular o momento de inércia e achar o valor de .
Passo 2
Primeiro vamos achar o termo . Esse termo é definido unicamente pelas condições dos apoios e segue sempre o mesmo padrão, e a gente viu na teoria que para o caso biengastado :
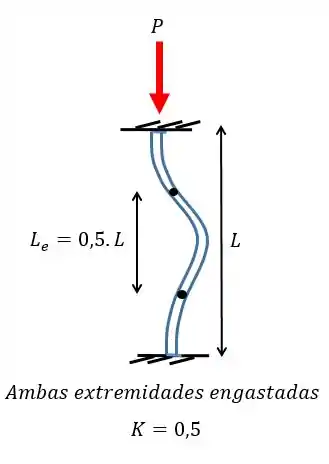
Pronto! Agora é só calcular o momento de inércia e partir pro abraço!
Passo 3
Pessoal, a flambagem sempre vai ocorrer no eixo de menor momento de inércia!! Se a gente for olhar na tabela para perfis de abas largas vamos ter, para o perfil :
obs: o eixo sempre vai ter o momento de inércia menor para este ripo de perfil. Então vamos utilizar
Passo 4
Agora é só substituir na equação da força crítica:
Passo 5
Agora vamos ver se a coluna não escoa. Como o aço tem , então a gente vai fazer:
A área do perfil também é retirada da tabela:
Então vamos ter:
Passou e muito do nosso limite de não é mesmo?
Então a coluna até suporta a flambagem, mas ela vai escoar devido à carga normal excessiva..
Resposta
A coluna não suporta a carga pois escoará!