Método da integração
Teoria
Equações e reações
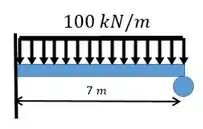
Fala aí, galerinha marota! Hoje a gente vai bater um papo sobre o tema vigas e eixos estaticamente indeterminados. Quando nós temos uma viga ou um eixo estaticamente indeterminado isso significa que não é possível achar todas as reações apenas pelas equações da estática, temos um sistema hiperestático, como o mostrado abaixo.
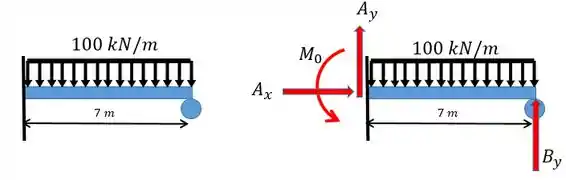
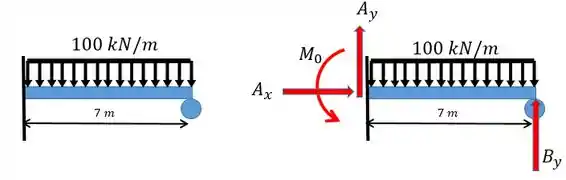
O carregamento mostrado na figura da esquerda possui as reações mostradas na figura da direita. É possível ver que existem 4 reações (duas forças no eixo vertical, uma no eixo horizontal e um momento devido ao engaste).
Mas aí que está a questão, se a gente fosse resolver esse problema apenas pelas equações da estática nós teríamos apenas 3 equações:
- Somatório das forças em
- Somatório das forças em
- Somatório dos momentos (aqui vamos fazer em relação ao ponto de engaste e considerar o sentido anti-horário positivo)
Perceba que se nós temos 4 incógnitas e 3 equações então o nosso sistema não pode ser determinado utilizando apenas essas três equações. Como vamos proceder então?
Vamos resolver isso utilizando a linha elástica!
Relembrando a linha elástica
Nós vamos poder resolver esse sistema com a ajuda da nossa amiga linha elástica.
Caso você já tenha esquecido da nossa miguxa, nós podemos calcular a linha elástica como:
Onde:
- é o coeficiente de elasticidade.
- é o momento de inércia.
- é a deflexão da linha elástica.
- a equação do momento fletor.
Agora vamos aprender como o método realmente funciona e é bem simples! O que vamos fazer é utilizar a equação da linha elástica para ter mais uma equação e com isso poder resolver o sistema. Na teoria é bem simples, na prática pode ser um pouco complicado, mas vamos fazer juntos com calma.
Cálculo do momento fletor
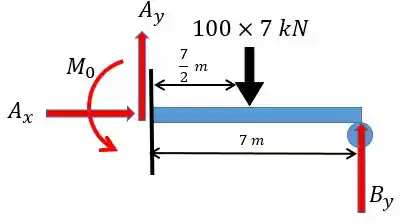
Que tal pegar o nosso exemplo inicial novamente? A gente tinha o seguinte:
Como a equação da linha elástica depende da equação do momento fletor, vamos achar essa equação. Para isso vamos realizar um corte na viga de forma a obtermos a força cortante e o momento fletor .
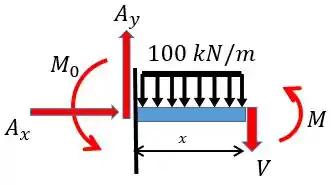
Pessoal, a gente quer a equação do momento fletor, correto? Então a gente precisa utilizar apenas a equação do somatório dos momentos. Além disso, a força cortante não nos interessa então para facilitar o cálculo vamos aplicar o somatório dos momentos em relação à extremidade direita da seção.
Abaixo vou mostrar apenas as forças que de fato causam momento, também está representado a força concentrada relativa ao carregamento uniforme:
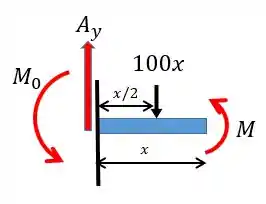
Vamos considerar o sentido anti-horário positivo e teremos
Isolando o momento fletor vamos ter a seguinte equação.
obs: talvez você esteja mais acostumado a utilizar com relação ao lado esquerdo, se for o caso pode fazer assim o resultado não vai mudar – o importante é colocar a força cortante em função das outras forças.
Cálculo da linha elástica
Essa é a parte mais importante e é só substituir a equação do momento na equação da linha elástica.
Galera, não se assustem com essa equação diferencial!
Sério, essa equação não é muito difícil de resolver não. Presta atenção, a gente vai simplesmente integrar dos dois lados em função de :
Lembrando que o termo é, na grande maioria das vezes, uma constante, logo nós vamos ter
E agora vamos integrar novamente
Aí agora você olha para isso e fala assim “não acredito ganhei uma equação, mas ela veio com mais duas incógnitas ( e ), não adiantou de nada!! Que ódioooo”
Mas calma, jovem, eu vou te contar um segredo. Existem as condições de contorno, elas vão salvar a pátria. Se liga no próximo passo como isso vai acontecer
Encontrando as condições de contorno
Para que a gente possa resolver a equação da linha elástica a gente precisa das condições de contorno. Essas condições consistem basicamente em saber quando a deflexão e quando a angulação são iguais a zero.
Além disso é importante lembrar que a angulação é igual à primeira derivada de
Resumindo as equações de contorno são as seguintes:
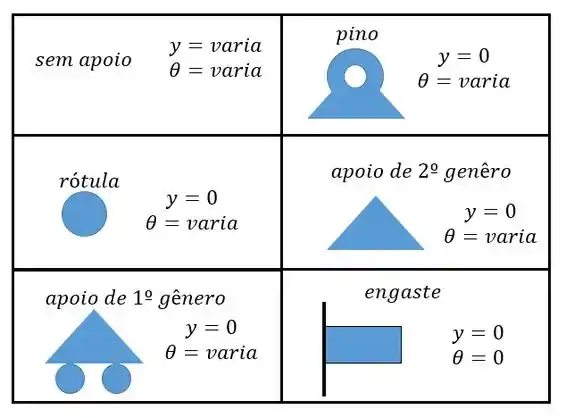
Olhando o nosso problema nós vamos ter que no lado esquerdo temos um engaste e no lado direito uma rótula:
Dessa forma temos três equações de contorno que refletem a linha elástica, representada abaixo:
Demorou!! Mas a gente fez isso para que mesmo? Se lembra da equação da linha elástica?
Como nós temos 3 pontos para substituir nessa equação a gente vai conseguir achar , e não vamos achar ou diretamente, mas vamos achar uma equação que relacione e . Essa equação vai ser a nossa 4ª equação (juntamente com as três da estática) que utilizaremos para achar todas as reações!!
Realizando a substituição
Primeiro vamos utilizar a equação da inclinação.
lembra que ? Então vamos ter:
Substituindo e
Agora vamos substituir na equação da deflexão.
Substituindo e
E finalmente substituindo e
Galera, percebam que a gente fez isso tudo só para achar mais uma equação que relaciona duas incógnitas lá do começo. Agora para achar as reações a gente tem que utilizar as 3 equações da estática.
Achando as reações
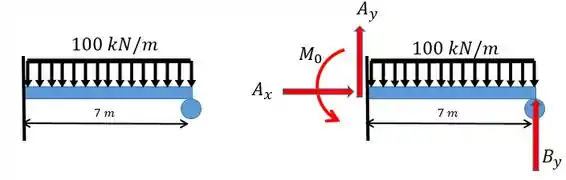
As três equações que a gente tinha lá do começo eram:
- Somatório das forças em
- Somatório das forças em
- Somatório dos momentos (aqui vamos fazer em relação ao ponto de engaste e considerar a sentido anti-horário positivo)
- Agora a gente tem a quarta equação!
Aí é só resolver o sistema:
Uhullll!!!! Achamos o nosso resultado! Viram que com o auxílio da linha elástica é possível achar as reações mesmo em vigas estaticamente indeterminadas? Claro que sim né!
Cálculo do momento fletor
Cálculo da linha elástica
Encontrando as condições de contorno
Realizando a substituição
Achando as reações
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.103 (Adaptado)
Determine as reações nos apoios e ; em seguida, trace o diagrama de momento fletor. Considere constante.
Passo 1
Faaala, galerinha!! Vamos resolver um exercício de vigas e eixos estaticamente indeterminados uhullll!!
O mais importante nesse problema é entender que ele não pode ser resolvido apenas pelas equações da estática porque é um problema hiperestático (tem um engaste e um apoio), então vamos utilizar a equação da linha elástica também, belezinha?
Então vamos começar fazendo o diagrama de corpo livre para entender como as reações são nesta questão e achar 3 equações. Depois a gente vai utilizar a equação da linha elástica como a nossa 4ª equação.
Então partiu!
Passo 2
Vamos começar fazendo o diagrama de corpo livre:
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica, que é a parte mais legal da questão!
Boa que usou meme!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Onde é a equação do momento fletor. Então a gente precisa saber como o momento fletor se comporta nessa viga. Nós vamos fazer isso pelo método convencional das seções, belezinha?
Então fazendo um corte nessa viga vamos ter:
Pessoal, como queremos apenas o momento fletor então a gente parte direto para a equação do somatório dos momentos. Além disso para não precisar calcular o valor da força cortante vamos considerar o ponto de aplicação bem no corte:
Pronto! Acabamos de achar a equação do momento fletor!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos integrar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Substituindo na 3ª equação:
Portanto vamos ter:
Passo 7
O problema também pediu para traçarmos o diagrama do momento fletor né? Se a gente já tem a equação, que foi achada no passo 3:
Substituindo os valores:
No diagrama vai ficar da forma:
Resposta
Reações:
Diagrama:
Exercício Resolvido #2
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.108 (Adaptado)
Determine as reações nos apoios e ; em seguida, trace o diagrama de momento fletor. Considere constante.
Passo 1
Faaala, galerinha!! Vamos resolver mais um probleminha de vigas estaticamente indeterminadas. Dessa vez uma força pontual atua na nossa viga e queremos achar as reações e fazer o momento fletor.
Para isso vamos começar fazendo o diagrama de corpo livre da nossa viga e achar a equação do momento fletor.
Com a equação do momento fletor nós vamos achar a equação da linha elástica
E com essa nova equação vamos poder resolver o sistema que antes era indeterminado.
Então partiu!
Passo 2
Vamos começar fazendo o diagrama de corpo livre:
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Utilizando funções de descontinuidade equação vai ser mais ou menos assim:
Mas como que chegamos nessa equação tão rápido? Vem comigo que vou explicar termo a termo:
- é o valor inicial do momento, sempre que temos um engaste a gente tem que adicionar o valor do momento relativo ao próprio engaste.
- é o termo relativo à força cortante. O sinal negativo aparece porque essa força ameniza o momento fletor, vale porque a cortante entre vale e temos o termo porque ela aumenta sua intensidade conforme anda na barra.
- é o termo relativo ao momento da força pontual que começa a aparecer apenas depois de .
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Como
Substituindo
Como
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que
Agora então:
Substituindo
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Passo 7
O problema também pediu para traçarmos o diagrama do momento fletor né? Se a gente já tem a equação, que foi achada no passo 3:
Substituindo os valores:
No diagrama vai ficar da forma:
Resposta
Reações:
Diagrama:
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.111 (Adaptado)
Determine as reações nos apoios e . Considere constante.
Passo 1
Pessoal!!! E aí, como vocês estão? Prontos para mais uma questão de vigas estaticamente indeterminadas?
Essa questão tras uma viga engastada em e apoiada em e o problema pede para acharmos as reações, que ao todo são 4. Como você já deve saber nós temos apenas 3 equações da estática para o caso bidimensional então vamos precisar de mais uma que vem da linha elástica:
E com essa nova equação vamos poder resolver o sistema que antes era indeterminado.
Então a gente tem que, essencialmente, achar a equação da linha elástica e depois resolver um sisteminha!
Passo 2
Vamos começar fazendo o diagrama de corpo livre:
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Vamos utilizar equações de descontinuidade e para isso fica mais fácil se fizermos para a força cortante primeiro:
Agora é só integrar e achar o momento
Onde é o momento no engaste
Assim vamos ter:
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Substituindo
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Resposta
Reações:
Exercício Resolvido #4
Elaboração própria
Determine as 4 equações que determinam as reações nos apoios e . Considere constante.
Passo 1
Fala, galera!!!
Novamente temos um problema onde a viga está estaticamente indeterminada (possui 4 reaçoes e 3 equações da estática) e vamos ter de utilizar a equação da linha elástica como a nossa 4ª equação.
Nesse problema em específico a carga uniforme começa a partir da distância então vai ser muito útil que utilizemos funções de descontinuidade para isso!
Vamos ver como isso vai ficar!!
Passo 2
Vamos começar fazendo o diagrama de corpo livre:
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Vamos utilizar equações de descontinuidade e para isso fica mais fácil se fizermos a equação do carregamento primeiro:
Para achar a força cortante vamos integrar:
Onde
Logo,
Agora é só integrar e achar o momento
Onde é o momento no engaste
Assim vamos ter:
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Substituindo
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resposta
Exercício Resolvido #5
Ferdinand P. Beer, E. Russell Johnston, Resistência dos Materiais, 3ª ed. São Paulo: MAKRON BOOKS, 1995, pp. 845. Exercício 8.9 (Adaptado)
Determine as reações nos apoios e , considerando o carregamento triangular imposto. Considere constante.
Passo 1
Faaala, galerinha!! Vamos resolver mais um probleminha de vigas indeterminadas.
Toda a questão vai girar entorno de dois pontos: o primeiro são as 3 equações da estática e o segundo a 4ª equação, proveniente da linha elástica. Com essas 4 equações é possível achar todas as reações dos apoios.
Passo 2
Vamos começar fazendo o diagrama de corpo livre já considerando a carga triangular como uma carga pontual, para isso a gente tem que lembrar que:
E que essa força atua no centro geométrico do triângulo ()
Observe que existem 4 reações e por isso que precisamos de 4 equações também. De qualquer forma vamos escrever as equações da estática para ver o que temos:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Onde é a equação do momento fletor. Para achar a equação do momento vamos utilizar funções descontinuas começando pela equação do carregamento:
Integrando para achar a força cortante:
Onde
Agora vamos integrar novamente
Onde
Obtendo
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No engaste:
Na rótula:
Perceba que na rótula a viga está livre para rotacionar!
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
obs: Perceba que vamos utilizar a equação da angulação () e não da deflexão (). Lembre também que
Essa é a nossa 4ª equação!! Agora é só voltar nas equações do passo 2 e resolver o sistema!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter:
Resposta
Reações:
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.104
Determine as reações nos apoios e ; em seguida, trace o diagrama de momento fletor. Considere constante. Despreze o efeito da carga axial.
Passo 1
E aí, meus amores, tudo bom? Vamos resolver mais um exercício sobre vigas e nesse exercício a gente já consegue ver logo de cara que temos dois engastes logo se trata de uma viga hiperestático (ou estaticamente indeterminado). Caso você não tenha reparado olha só o diagrama de corpo livre dessa viga como fica:
Reparem que o problema pediu para negligenciarmos as forças na horizontal, mas mesmo assim ainda temos 4 incógnitas para apenas três equações. Sendo assim, vamos precisar de mais uma equação para resolver essa questão.
Essa quarta equação será extamente a equação da força elástica. Que é dada por:
Então partiu resolver!!
Passo 2
A partir do nosso diagrama de corpo livre vamos achar as três primeira equações.
- Para a viga vertical:
- Para a viga horizontal não precisamos fazer já que negligenciaremos essa viga.
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Show! Temos duas na verdade já que deixamos a equação referente à horizontal de lado. Então vamso precisar de mais duas equações. Elas serão a da deflexão e da inclinação .
Passo 3
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Onde é a equação do momento fletor. Então a gente precisa saber como o momento fletor se comporta nessa viga. Aqui vamos utilizar uma função de descontinuidade, caso você não esteja lembrando direito não se preocupe vamos fazer isso bem devagar e seguindo a tabelinha abaixo:
Essa viga possui dois momentos, como o momento fletor dado por uma carga-momento é dado, conforme a tabela, por:
Então para o nosso caso nós vamos ter:
Mas a viga não é composta só pelos momentos correto? Também temos as três forças. A tabela nos fornece que o momento fletor dado por uma força é do tipo:
Para as nossas três forças nós vamos ter:
Então o nosso momento fletor da viga como um todo é dado pelos momentos puros mais o momentos das forças:
Pessoal, aqui vale uma observação! Como na função de descontinuidade quando temos um termo negativo dentro do parêntesis bonitinho esse mesmo termo se torna nulo na realidade. Então nós podemos tirar os termos que aparecem porque esses termos sempre serão iguais a zero.
Sendo assim nossa equação fica da forma:
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições referentes aos dois engastes:
Na esquerda:
Na direita:
Belezinha! Agora é só substituir essas quatro condições de contorno na equação que temos da linha elástica!
Lembrando que os termos dentro do parêntesis bonitinho que sejam negativos serão desconsiderados, logo obtemos:
Substituindo:
obs: Perceba que vamos utilizar a equação da angulação () e não a da deflexão (). Lembre também que .
Substituindo e negligenciando os termos que seriam negativos dentro dos parêntesis:
Perceba que a gente já consegue achar a equação da linha elástica porque já encontramos nossas duas constantes. Mas a gente quer mais duas equações correto? Então vamos continuar com as condições de contorno.
Passo 6
Agora como então não tem termo negativo dentro dos parêntesis, assim não podemos negligencia-los.
Reorganizando:
Reorganizando:
Repare que agora encontramos mais duas equações exatamente como queríamos!
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Passo 7
O problema também pediu para traçarmos o diagrama do momento fletor né? Colocando os resultados que achamos na nossa viga fica mais fácil de fazer:
Resposta
Reações:
Diagrama:
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.117
Determine as reações nos apoios e trace os diagramas de força cortante e momento fletor. é constante. O apoio é um mancal de encosto.
Passo 1
E aí, pessoal!! tranquilão com vocês? Olha essa questão de eixo que bacana, para a gente entender ela direitinho é importante notar que o mancal de enconsto vai ser o único que possui reação na horizontal beleza? Então se a gente fizer o diagrama de corpo livre vamos ter algo mais ou menos assim:
Aí perceba que temos 4 incógnitas e só temos 3 equações da estática para resolver esse tipo de problema. Então estamos falando de um eixo estaticamente indeterminado.
Para resolver problemas assim nós vamos utilizar nosso conceito de linha elástica porque assim vamos ter mais uma equação e conseguimos resolver o problema!!! Só pra lembrar que a linha elástica é dada por:
Então partiu resolver!
Passo 2
Nós já fizemos o diagrama de corpo livre e agora vamos utilizar as três equações das estática para determinar o máximo de relações possíveis:
Utilizando as três equações vamos ter:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Pessoal, aqui a gente meio que tem que utilizar funções de descontinuidade porque caso contrário iremos fazer muuuuita conta. Mas pode ficar tranquilo, vamos fazer juntos e ainda vou te dar uma tabelinha aqui pra te ajudar:
Como nesse problema temos apenas forças então todos os momentos serão da forma:
Vamos fazer devagarinho:
- Para a força em vamos ter:
- Para a força em vamos ter:
- Para a força vamos ter:
- Para a força em vamos ter:
Perceba que a força está no sentido positivo, logo o sinal do momento também é positivo. Além disso a força atua em .
obs: Como esse é o último termo a gente poderia ignorar, mas na real não faz diferença colocar ou não ok?
Então agora é só somar todos os termos:
Prontinho, temos nossa função do momento fletor escrita em termos de função de descontinuidade!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez.
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No ponto :
No ponto
No ponto :
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Como podemos eliminar alguns termos e irá sobrar:
Substituindo
Como , novamente poderemos retirar alguns termos o obter:
Substituindo:
Agora a gente pode retirar o termo ou não tanto faz!! De qualquer maneira vai dar zero.
Substituindo então vamos ter:
Reorganizando nós temos:
Perceberam que agora temos mais uma equação? Essa equação junto com aquelas lá de cima vão fornecer os valores de .
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
Passo 7
O problema também pediu para traçarmos os diagramas da força cortante e do momento fletor né? A equação do momento fletor a gente já tem:
Substituindo os valores:
Ou podemos também jogar direto os valores das reações no eixo e obter o diagrama que vai ficar da forma:
Passo 8
Para achar o diagrama da força cortante é só derivar o momento:
Derivando:
Da mesma forma podemos utilizar as reações direto no eixo e obter:
Resposta
Reações:
Diagrama do momento fletor:
Diagrama da força cortante:
Exercício Resolvido #8
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.109
Determine as reações nos apoios e a seguir trace os diagramas de força cortante e momento. é constante.
Passo 1
Fala aí, galerinha!! Essa questão nos fornece uma viga apoiada em dois roletes e e num pino . Além disso, a viga possui um carregamento triangular e nos é pedido que achemos as reações dos apoios e os diagramas de força cortante e momento fletor.
Se montarmos o diagrama de corpo livre vamos ter o seguinte:
Primeiro é importante ressaltar que temos 4 forças de reação e por isso trata-se de um viga estaticamente indeterminada. Consequentemente, vamos ter de utilizar a equação da linha elástica como na nossa quarta equação. Caso não lembre a equação é dada por:
Então partiu resolver!
Passo 2
Nós já fizemos o diagrama de corpo livre e agora vamos utilizar as três equações das estática para determinar as três primeira equações:
Perceba que o carregamento triangular foi dividido em dois carregamentos, também triangulares, e simétricos a qual cada um exerce uma força de valor . Onde cada força tem o valor de:
Utilizando as três equações vamos ter:
- Para o eixo vertical:
- Para o eixo horizontal:
- Para o momento:
Aqui vamos aplicar o momento em relação ao ponto e considerar o sentido anti-horário positivo.
Percebam que a única força que podemos achar com essas equações é a força , que é nula, fora isso não temos mais muito o que fazer. Então partiu pra linha elástica!
Passo 3
Agora vamos achar a equação da linha elástica. Essa é a parte mais crucial da questão!
Para achar a linha elástica a gente precisa lembrar da equação, caso você não lembre é essa aqui:
Então a gente precisa da equação do momento fletor . Para tal vamos fazer um corte e obter:
Agora temos de achar a equação que define o carregamento. A gente sabe que quandi o carregamento também vale zero e quando o carregamento vale . Como trata-se de uma variação linear então vamos ter:
Show! Agora é só aplicar o somatório dos momentos exatamente no ponto do corte (fazemos isso para não precisar calcular a força cortante). Considerando o sentido anti-horário positivo:
Lembrando que a força concentrada vale a metade do carregamento máximo vezes o comprimento:
E atua numa distância de do ponto , sendo assim:
Logo, a equação do momento fleotr pode ser dada por:
Prontinho, temos nossa função do momento fletor!
Passo 4
Vamos substituir a equação do momento fletor lá na nossa equação da linha elástica!
Agora vamos derivar a primeira vez.
lembrando que o valor é uma constante.
Pessoal, essa é a equação da angulação belezinha? Lembrem-se !
Continuando vamos fazer a segunda integração.
Show de bola! Achamos nossa equação da linha elástica mas ainda temos de achar o valor das constantes e . Para isso vamos utilizar as condições de contorno relativos aos apoios!
Passo 5
As condições de contorno são dadas pela nossa tabelinha!
Então nós vamos ter as seguintes condições de contorno.
No ponto :
No ponto
No ponto :
Belezinha! Agora é só substituir essas três condições de contorno na equação que temos da linha elástica!
Reorganizando nós temos:
Perceberam que agora temos mais uma equação? Essa equação junto com aquelas lá de cima vão fornecer os valores de .
Passo 6
As equações que temos então são:
Resolvendo nós vamos ter que:
A primeira parte do problema já foi, agora é só achar os diagramas!
Passo 7
Para achar os diagramas vamos colocar os dados que achamos na nossa viga:
Assim, para fazer o diagrama da força cortante basta lembrar que quando temos um carregamento triangular a cortante é uma função de terceiro grau:
Passo 8
Para achar o diagrama da força cortante é só aplicar a equação que já achamos:
Agora sabemos o valor de :
Resposta
Reações:
Diagrama da força cortante:
Diagrama do momento fletor:
