Método dos momentos de área
Produzido por Pablo RicardoTeoria
Fala, pessoal!!
Que tal aprender mais um método de resolução para vigas e eixos estaticamente indeterminados hein?
Galera, deixa eu falar uma coisa para vocês: a equação da linha elástica fornece mais uma equação de forma que podemos resolver problemas hiperestáticos!!!! Agora vamos ver como resolver isso mas sem focar muito na equação e focando principalmente no diagrama .
Dessa vez vai ser o diagrama que vai nos ajudar a achar as resultantes.
Separação dos componentes
Acho que um bom jeito de começar é fazermos esse diagrama para um exemplo prático, você concorda? Segue o exemplo:
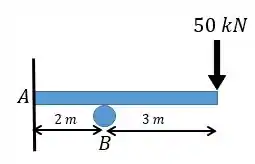
Pessoal, a gente não consegue achar diretamente o diagrama , mas o que a gente pode fazer é dividir esse problema em dois. Vamos fazer isso substituindo o apoio por uma força de reação .

Agora que os componentes estão separados vamos fazer o diagrama de cada um deles.
Diagrama
Para cada carregamento diferente vamos fazer o respectivo diagrama de momento fletor.
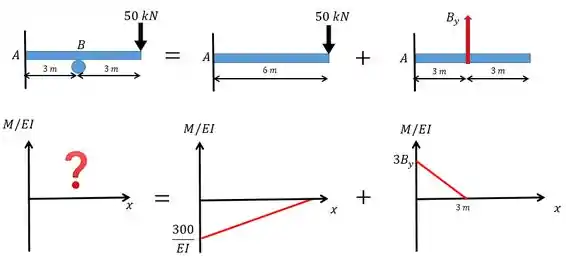
Nosso gráfico final fica com a seguinte forma
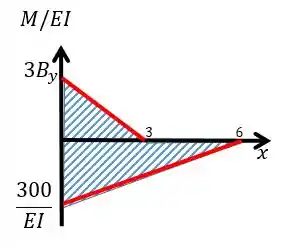
Esboçar a linha elástica
Pessoal, agora a gente vai achar uma resultante (no nosso caso ). Para fazer isso a gente precisa utilizar a linha elástica e estar ligado nas condições de contorno do nosso problema, se a gente olhar a nossa tabela vamos ter:
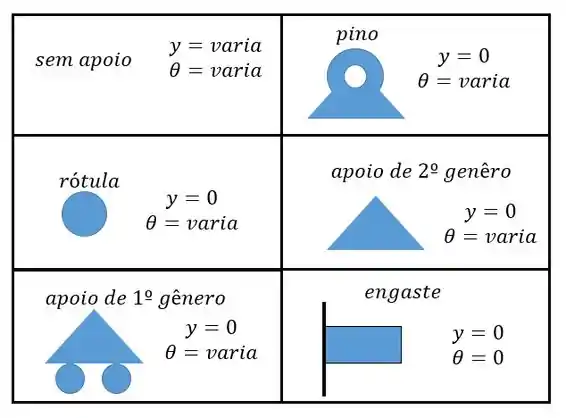
Assim, no engaste vamos ter:
No apoio:
Com isso podemos fazer um esboço da nossa linha elástica.

Percebam que, em , tanto a inclinação quanto a deflexão são nulas em relação ao original (em verde) e em a deflexão é nula, porém, há uma certa angulação. Exatamente como as condições de contorno descrevem.
Aplicar a equação para achar uma das reações
Lembrando da linha elástica nós temos que a deflexão relativa é dada por.
Ou seja, a diferença entre a deflexão do ponto em relação ao ponto é igual ao centroide da área do gráfico vezes a área do gráfico. Observe:
IMPORTANTE: Como nós queremos e deflexão de em relação à então vamos fazer as áreas nesse mesmo intervalo até
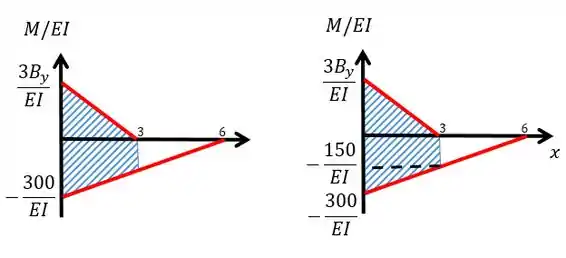
De modo a facilitar a conta nós vamos dividimos essa área em dois triângulos e um retângulo. Agora é só achar o centroide de cada figura a e sua área.
- Triângulo superior
- Triângulo inferior
- Retângulo
Agora vamos somar tudo!
Como a deflexão em e é igual então vamos ter que
Logo,
Olha que incrível galera!!! Achamos uma das reações sem nem utilizar as equações da estática!
Achar as outras reações
Para achar as outras reações agora sim recorremos à estática. Fazendo o diagrama de corpo livre:
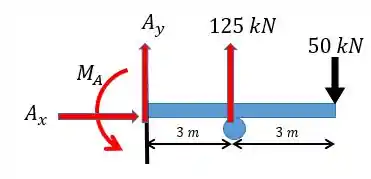
Para o somatório das forças em :
Para o somatório das forças em :
Finalmente aplicando o somatório dos momentos no ponto :
Achamos todas as reações!!!
Resumo
Logo, para que a gente possa utilizar esse método temos de seguir o seguinte passo a passo:
- Separar os componentes.
- Fazer o diagrama .
- Esboçar a linha elástica.
- Aplicar a equação da deflexão ou inclinação relativa entre dois pontos específicos.
- Achar o valor de uma das reações.
- Achar as outras reações pelas equações da estática.
Diagrama M / E I
Esboçar a linha elástica
Aplicar a equação para achar uma das reações
Achar as outras reações
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 460. Problema 12.111 (Adaptado)
Determine as reações nos apoios e . Considere constante.
Passo 1
Faaala, galera!!! E aí como vocês estão, prontos para começarem uns exercícios de método dos momentos de áreas aplicado a vigas estaticamente indeterminadas? Tenho certeza que sim!!!
Vamos lá, então pessoal! Como o próprio tópico já diz estamos falando de vigas estaticamente indeterminadas, isso significa dizer que as reações das vigas não podem ser calculadas com base apenas nas equações da estática, logo a gente vai precisar de mais uma ferramenta para isso.
Essa ferramenta é o diagrama aliado com um certo conhecimento da linha elástica. Vamos ver como isso nos ajudará!!
Passo 2
Vamos começar transformando o carregamento em dois carregamentos mais simples:
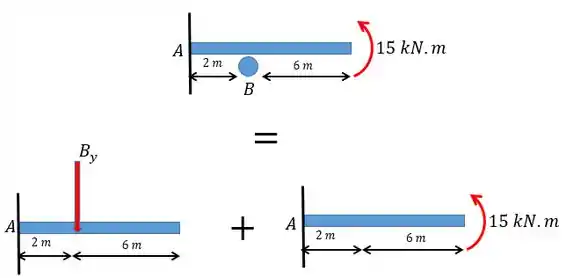
Perceba que não mudamos o carregamento! A única coisa que fizemos foi tirar o apoio e aplicar uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
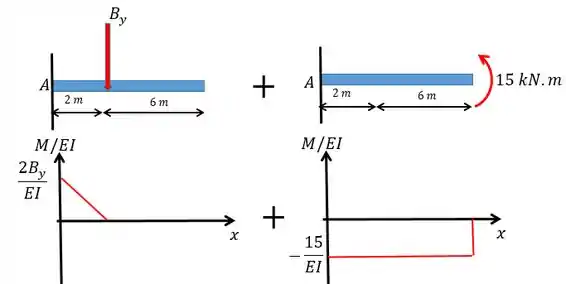
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:
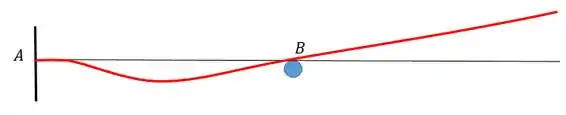
As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
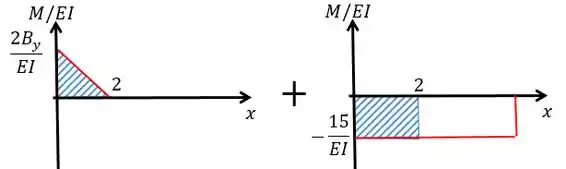
Como temos mais de uma figura:
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
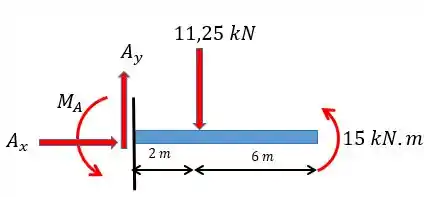
Podemos ver que:
Resposta
Exercício Resolvido #2
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.114
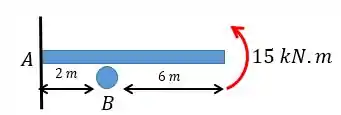
Determine as reações ao momento nos apoios e ; a seguir trace os diagramas de força cortante e momento fletor. é constante.
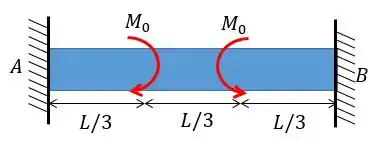
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas.
O primeiro passo vai ser sempre o mesmo, colocar as reações dos apoios e montar o nosso querido diagrama do corpo livre:
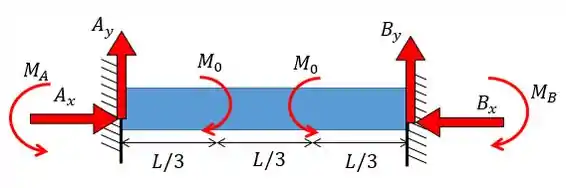
Repara que aqui, nós temos 6 incógnitas que são as reações nos nossos apoios, com isso, precisaríamos de 6 equações para determinar essa viga.
Mas repara só no seguinte, os momentos aplicados na nossa viga possuem o mesmo valor e estão aplicados em pontos simétricos, portanto, podemos dizer que há uma simetria na nossa viga.
Por isso,
Como não existem esforços verticais nem horizontais, não haverá reações nessas direções, portanto:
Com isso, ficamos apenas com duas incógnitas ( e) e uma equação (somatório dos momentos), o que resulta em problema estaticamente indeterminado e para resolve-lo, vamos seguir o passo-a-passo!
- Determinar as equações da estática
- Elaborar os diagramas
- Analisar as condições de contorno das linhas elásticas
- Utilizar o métodos dos momentos de área para calcular uma reação
- Com o valor dessas reações calcular as demais.
Passo 2
Vimos no Passo 1, que só iremos usar a equação do somatórios dos momentos que nesse caso, será:
- Momento
E como sabemos que o é zero, teremos então:
Logo, precisamos de apenas mais uma equação para resolver o problema e essa equação é a da linha elástica!
Passo 3
Agora a gente vai fazer o diagrama , a gente vai fazer isso somando os diagramas de cada carregamento.
Lembrando que vamos adotar aqui o sentido anti-horário como positivo!
Vamos começar nosso gráfico com o momento igual à que é o momento do engaste em . Ao chegar em , subtraímos com o momento dado pelo carregamento nesse ponto que é no sentido horário.
Depois, ao chegar em , somamos novamente o , pois agora o carregamento está no sentido anti-horário. E por fim, finalizamos o nosso gráfico, chegando em , quando subtraímos o momento , que sabemos que é igual a e por isso o nosso gráfico vai pra zero.
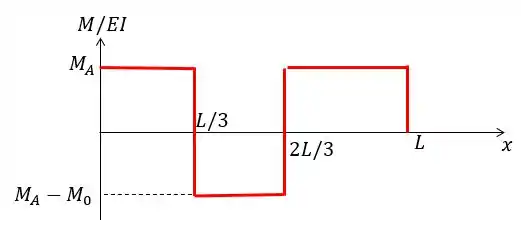
Passo 4
Beleza! A gente já tem os diagramas, agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar a nossa próxima equação!
Para isso vamos utilizar as condições de contorno que são:
No engaste :
No engaste
Então, uma coisa que podemos fazer é aplicar a equação do momento de área entre os pontos e e assim vamos achar a inclinação relativa entre eles. Lembrando:
Ah, e se liga, a inclinação relativa entre e vai ser zero, afinal e .
Vamos, encontrar agora essa área:
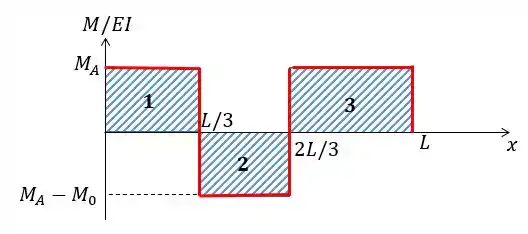
Agora é só fazer a área dessas figuras:
- Da figura número 1:
- Da figura número 2:
- Da figura número 3:
Passo 5
Então somando todos esses termos vamos ter:
Pessoal, normalmente quando uma área está localizada abaixa do eixo a gente tem que colocar um sinal negativo na sua frente, mas como o termo já é negativo, porque é maior do que então não vamos fazer isso nesse caso, beleza?
Mas a inclinação relativa entre e é zero, correto? Então vamos ter:
E sabemos que , logo:
Passo 6
Como o problema pede apenas as reações ao momento e vimos que:
Nós vamos ter como resultado:
Resposta
Exercício Resolvido #3
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.115 (Adaptado)
Determine as reações nos apoios e . Considere constante.
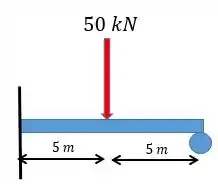
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar transformando o carregamento:
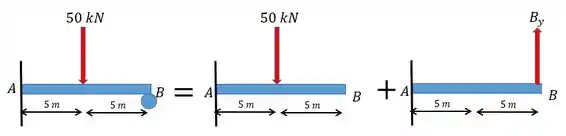
Perceba que não mudamos o carregamento! A única coisa que fizemos foi tirar o apoio e aplicar uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
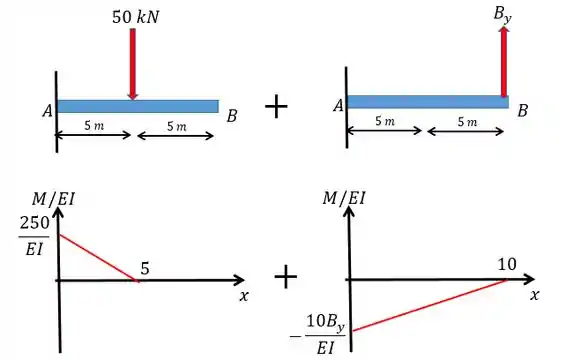
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:

As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
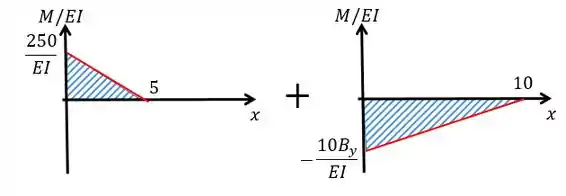
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todos as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
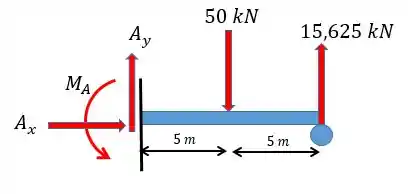
Podemos ver que:
Resposta
Exercício Resolvido #4
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.116 (Adaptado)
Determine as reações nos apoios e e trace o diagrama de momento fletor. Considere constante.
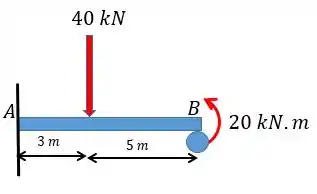
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar transformando o carregamento:
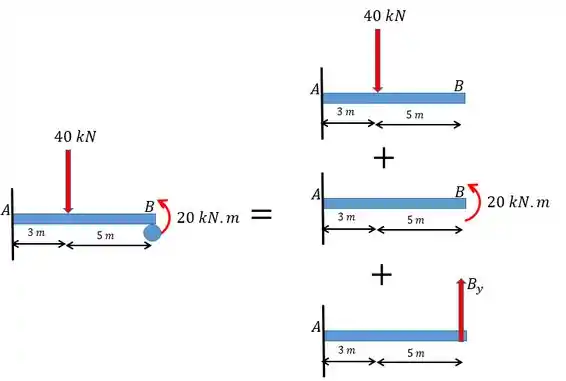
Perceba que não mudamos o carregamento, apenas segregamos em diferentes figuras e retiramos o apoio e o substituímos por uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
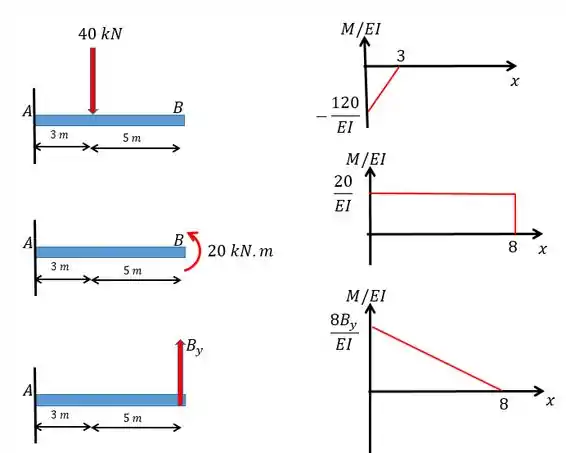
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:

As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
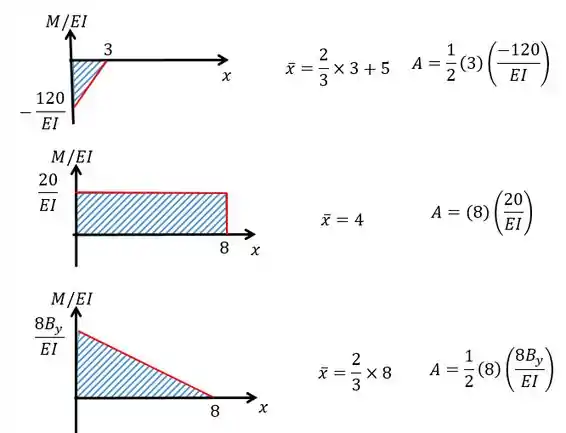
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
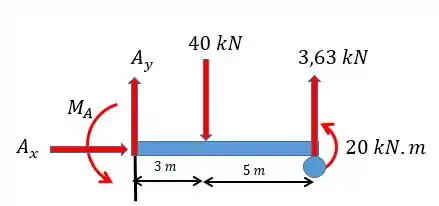
Podemos ver que:
Passo 7
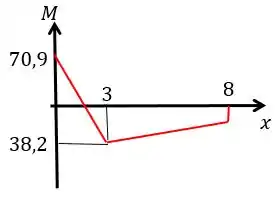
Fazere o diagrama de momento fletor:
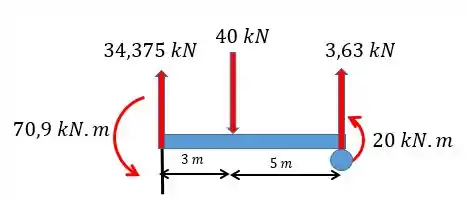
E o diagrama fica da forma:
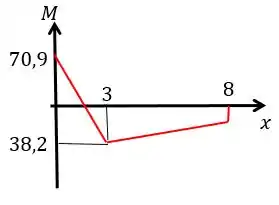
Resposta
Exercício Resolvido #5
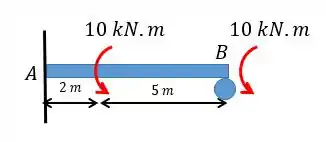
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.118 (Adaptado)
Determine as reações nos apoios e . Considere constante.
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar transformando o carregamento:
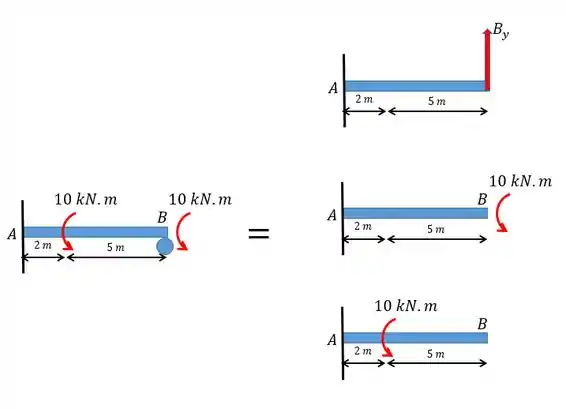
Perceba que não mudamos o carregamento, apenas segregamos em diferentes figuras e retiramos o apoio e o substituímos por uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
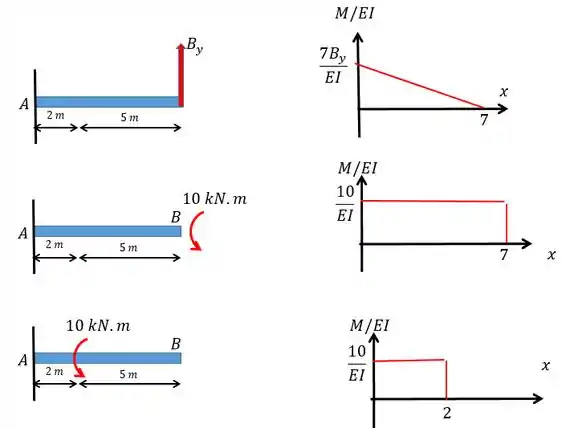
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo está um esboço da linha elástica, nesse caso específico a linha elástica assume uma forma bastante incomum mas não se espante o que precisamos saber é que não há deflexão relativa entre e :

As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
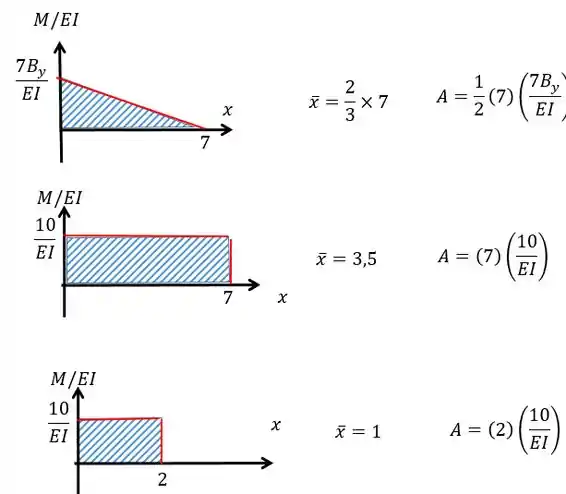
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
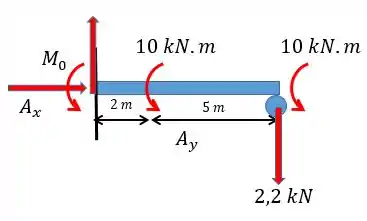
Podemos ver que:
Resposta
Exercício Resolvido #6
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.118
Determine as reações nos apoios. Considere constante.
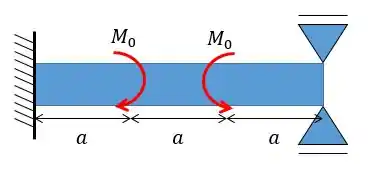
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar montando o diagrama de corpo livre:
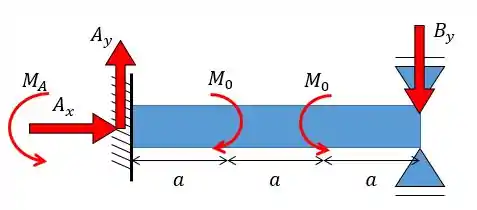
Agora vamos aplicar as equações da estática:
- Forças horizontais
- Forças verticais
- Momento
Porém, percebam que temos mais incógnitas do que equações logo vamos utilizar nosso conhecimento de linha elástica para achar mais uma equação!
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
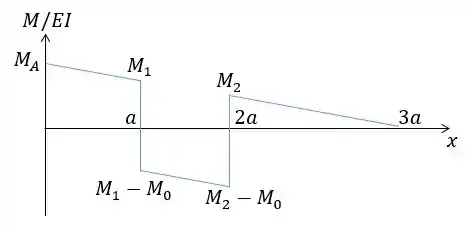
Onde:
Então vamos ter:
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar a nossa próxima equação!
Para isso vamos utilizar as condições de contorno que são:
No engaste :
No apoio
Então uma coisa que podemos fazer é aplicar a equação do momento de área entre os pontos e e assim vamos achar a deflexão relativa entre eles. Lembrando:
E o gráfico vai ser:
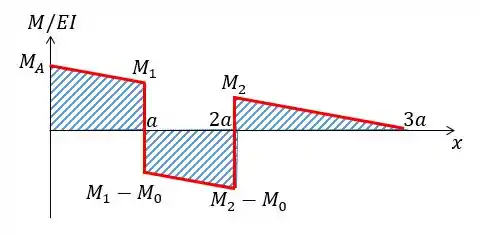
Passo 5
Agora vamos aplicar a equação fornecida no passo anterior e achar a deflexão relativa. Eu gosto de ao invés de trabalhar com trapézios sempre trabalhar com um retângulo mais um triângulo beleza? Então nós vamos ter 5 figuras:
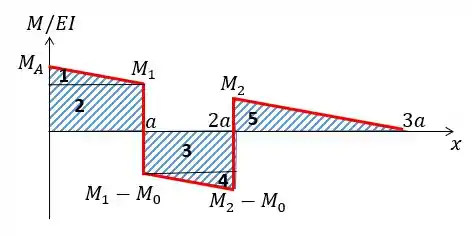
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
- Para a figura número 1:
- Para a figura número 2:
- Para a figura número 3:
- Para a figura número 4:
- Para a figura número 5:
Agora temos de somar os 5 termos e obter:
Como ambos os pontos possuem deflexão igual a zero então vamos ter:
Logo,
Passo 6
Agora é só utilizar essa equação que achamos em conjunto com as outras três do início do problema que vamos encontrar todas as reações:
Um modo de resolver é colocar todos os termos em função de :
Resolvendo essa equação vamos encontrar:
Resposta
Exercício Resolvido #7
R. C. Hibbeler, Resistência dos materiais, 7ª ed. São Paulo: Pearson, 2009, pp. 465. Problema 12.117 (Adaptado)
Determine as reações nos apoios e . Considere constante.
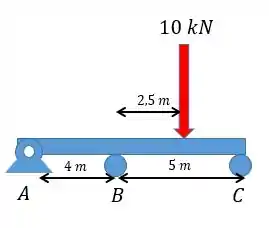
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas
- Analisar as condições de contorno da linhas elástica
- Utilizar o métodos dos momentos de área para calcaular uma reação
- Com o valor dessa reações calcular as demais.
Passo 2
Vamos começar transformando o carregamento:
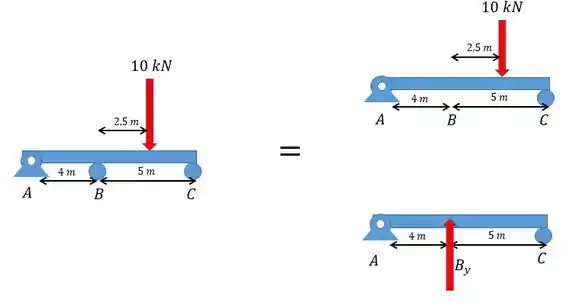
Perceba que não mudamos o carregamento, apenas segregamos em diferentes figuras e retiramos o apoio e o substituímos por uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
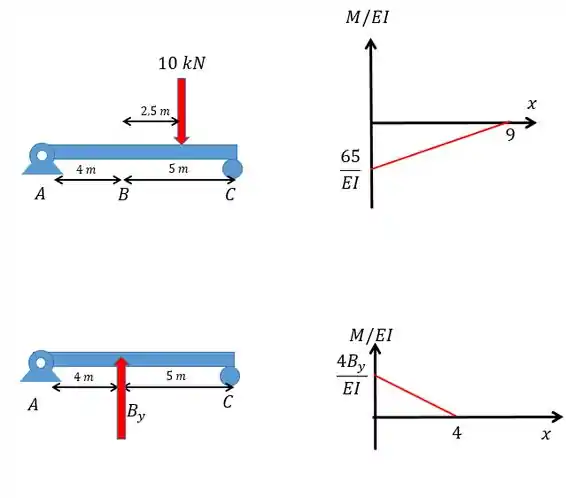
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo está um esboço da linha elástica:
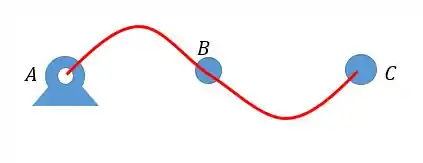
As condições são as seguintes:
em A :
em
em
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à que vai ser dada pelas áreas das figuras formadas nos gráficos:
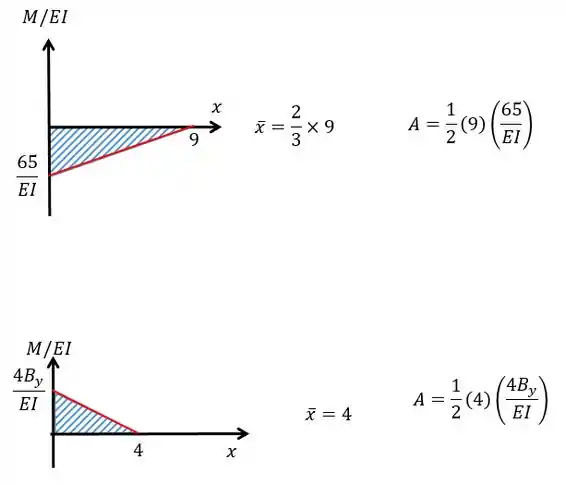
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
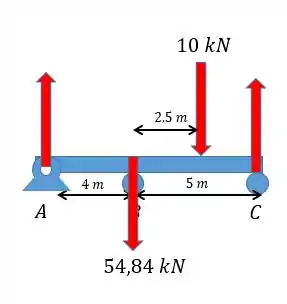
Podemos ver que:
Resposta
Exercício Resolvido #8
Elaboração própria
Determine as reações nos apoios e . Considere constante.
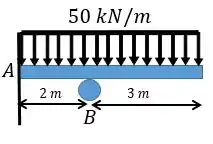
Passo 1
Bom pessoal, vamos resolver mais um problema de vigas estaticamente indeterminadas. Lembrando que vamos seguir o procedimento:
- Transformar o apoio em uma força e dividir os carregamentos.
- Elaborar os diagramas .
- Analisar as condições de contorno da linhas elástica.
- Utilizar o métodos dos momentos de área para calcaular uma reação.
- Com o valor dessa reações calcular as demais.
Passo 2
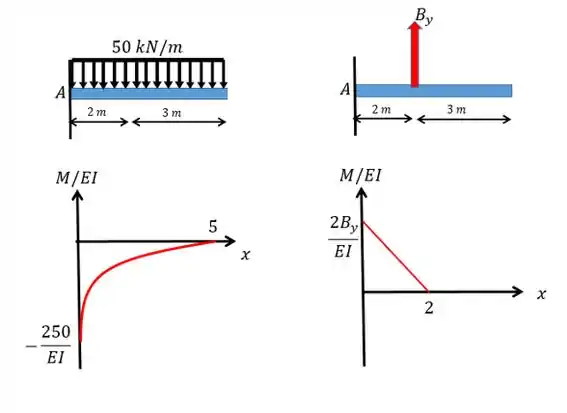
Vamos começar transformando o carregamento:
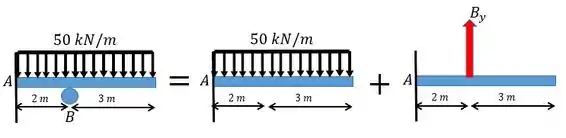
Perceba que não mudamos o carregamento, apenas segregamos em diferentes figuras e retiramos o apoio e o substituímos por uma força que é a força de reação.
Passo 3
Agora a gente vai fazer o diagrama a gente vai fazer isso somando os diagramas de cada carregamento.
Passo 4
Beleza! A gente já tem os diagramas agora a gente vai utilizar o conceito de linha elástica para nos ajudar a resolver a questão e achar o valor de .
A gente tem que saber como vai ser a configuração da linha elástica e principalmente as condições de contorno. Abaixo vamos representar um esboço da linha elástica:
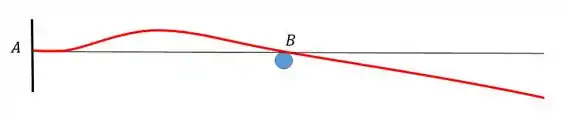
As condições são as seguintes:
No engaste :
Na rótula
Passo 5
Agora vamos utilizar essas condições de contorno para achar o valor de vamos fazer isso utilizando o método dos momentos das áreas para a linha neutra.
Repare que queremos a deflexão de em relação à , , que vai ser dada pelas áreas das figuras formadas nos seguintes gráficos:
- O primeiro é um triângulo então não tem muito segredo, basta lembrar que estamos olhando da perspectiva do ponto então as distâncias serão a partir desse ponto:
- Já para o segundo gráfico temos uma parábola. Assim como no anterior a perspectiva é sobre o ponto , mas vale ressaltar que a área e o centro de massa de uma parábola deste tipo são:
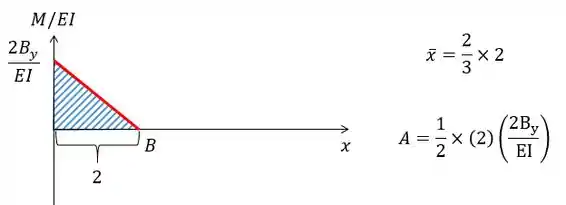
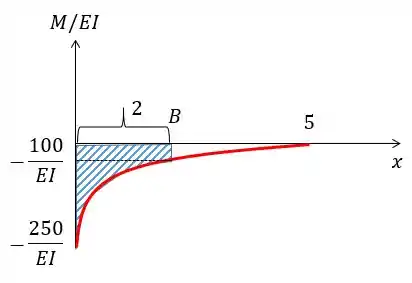
Como a nossa parábola não está completa vamos fazer o total (de 0 a 5) menos a parte branca (de 2 a 5).
Como temos mais de uma figura:
Lembre-se que o ponto que estamos analisando está centrado em , logo, todas as distâncias são referentes a esse ponto.
Como, pelas condições de contorno a deflexão em é igual à deflexão em vamos ter que:
Sendo assim,
Passo 6
Agora é só utilizar as equações da estática para achar o resto das reações, fazendo o diagrama de corpo livre:
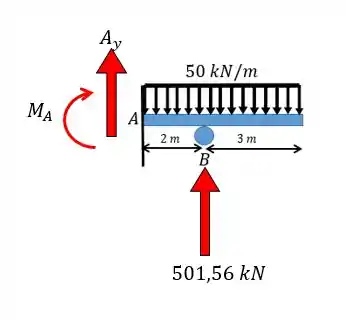
Podemos ver que:
Resposta