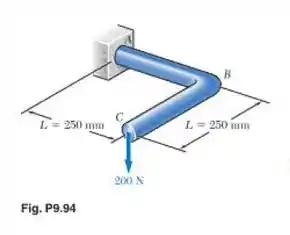
Uma barra de 16 mm de diâmetro foi moldada assumindo a forma mostrada. Determine a deflexão da extremidade C após lhe ser aplicada uma carga de 200 N. Use E = 200 GPa e G = 80 GPa.

Tá legal! Vamos começar pelas propriedades geométricas, no caso de uma seção circular, o momento polar de inércia será dado por:

Em que é o raio da seção. Então no nosso caso teremos:

E, sabemos que o momento de inércia se relaciona com o momento polar através da seguinte equação:

Então, substituindo o valor que encontramos para o momento polar, teremos:

Beleza, agora, sabemos que a rotação em B devido a torção será dada por:

Em que T é a torção aplicada, L é o comprimento do braço, J é o momento polar de inércia e G é o módulo de cisalhamento. Então, no nosso caso, a torção será a força de 200 N vezes o braço de alavanca L, ou seja:

Substituindo essa relação na equação acima, teremos a seguinte relação para a rotação no ponto B:

Agora, com essa rotação, a deflexão em C devido a porção CB será:

Beleza! Agora, nós vamos lá para o apêndice D do livre para pegar as deflexões em C devido ao carregamento em AB e em BC. Então, no nosso caso, temos o caso 1 do apêndice D para as duas porções da viga, onde a deflexão máxima, que ocorre na ponta, que é onde estamos interessados, é dada por:

Então, nos dois casos, tanto para a deflexão devido ao carregamento em AB e em BC, teremos essa deflexão, ou seja:

Agora que temos as 3 deflexões, a deflexão resultante será dada por:

Substituindo as expressões encontradas no passo 3, teremos:

Substituindo os valores conhecidos, chegamos em:

Shoow! Terminamos mais um, valeeu!