Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 37
Sabendo que o coeficiente de atrito estático entre o colar e a barra é 0,40, determine o intervalo dos valores de M para que o equilíbrio seja mantido quando e .
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para o membro AB:
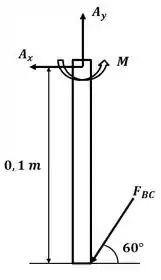
Agora vamos aplicar o somatório de momento em relação ao ponto A:
Passo 2
Agora vamos desenhar o diagrama de corpo livre para o colar C supondo que o movimento ocorre para cima:
Sabendo que a força de atrito pode ser escrita como , podemos aplicar primeiro o somatório de forças na direção :
Aplicando o somatório de forças na direção :
Substituindo esse valor na relação para encontrada no passo 1:
Passo 3
Agora vamos desenhar o diagrama de corpo livre para o colar C supondo que o movimento ocorre para baixo:
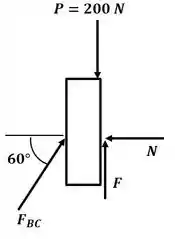
Sabendo que a força de atrito pode ser escrita como , podemos aplicar primeiro o somatório de forças na direção :
Aplicando o somatório de forças na direção :
Substituindo esse valor na relação para encontrada no passo 1:
Então, deve estar no seguinte intervalo: