Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 10

10- O cilindro hidráulico é usado para afastar as conexões e elevar a carga m . Determine a força compressiva C no cilindro, para a posição mostrada. Despreze a massa de todas as partes, a exceção de m .

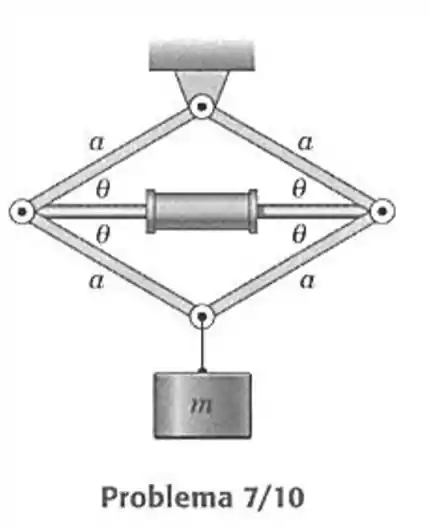
Passo 1

O cilindro hidráulico faz força nos dois extremos de forma que temos o seguinte sistema de forças.

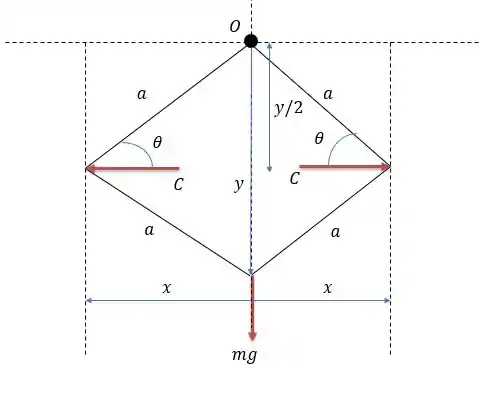
As duas forças C do cilindro hidráulico fazem a reta x esticar, logo o trabalho virtual dessa força será:

δ U C = C δ x + C δ x = 2 C δ x

E o trabalho virtual causado pela força peso faz esticar a reta y , logo seu trabalho virtual será:

δ U w = m g δ y

Logo o trabalho virtual total do sistema será:

δ U = δ U C + δ U w = 2 C δ x + m g δ y = 0

Note que fizemos a somatória dos trabalhos para o mesmo ponto O .

Passo 2

Agora para calcular o valor de x temos que fazer:

cos ⁡ θ = x a → x = a cos ⁡ θ

E o de y :

sin ⁡ θ = y 2 a → y = 2 a sin ⁡ θ

Substituindo esses valores na somatória de trabalhos virtuais nós teremos:

2 C δ ( a cos ⁡ θ ) + m g δ ( 2 a sin ⁡ θ ) = 0

Fazendo essa derivada:

2 a C × - sin ⁡ θ δ θ + 2 a m g cos ⁡ θ δ θ = 0

Isolando C :

2 a m g cos ⁡ θ = 2 a C s i n   θ

m g   c o t g   θ = C

Resposta

C = m g   c o t g   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Voltando ao Problema 10.45 e usando o valor encontrado para a força exercida pelo cilindro hidráulico BD, determine a mudança no comprimento de BD necessária para se elevar a plataforma presa em C em
Representado por μ s , o coeficiente de atrito estático entre o colar C e a haste vertical, deduza uma expressão para a intensidade do maior binánrio M para o qual o equilíbrio é mantido na posição mo
Determine o movimento horizontal do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Ver dica para o Problema 10.57.)
Deduza uma expressão para a eficiência mecânica do macaco discutido na Seção 8.6. Mostre que, se o macaco tem que ser autotravante, a eficiência mecânica não pode exceder 1 2 .
Usando o método do trabalho virtual, determine separadamente a força e o binário que representa a reação em H.