Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 27
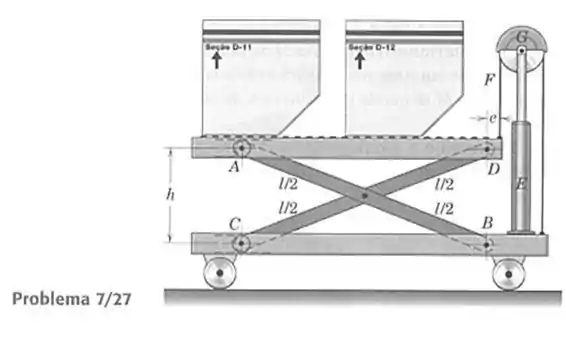
27- O projeto existente de um carrinho para colocação de carga em aviões está sob revisão. A plataforma do carrinho é elevada até a altura adequada pelo mecanismo mostrado. Existem dois sistemas de conexão e dois macacos hidráulicos, um de cada lado. Os cabos que levantam a plataforma são controlados pelos cilindros hidráulicos , cujas barras dos pistões levantam as polias . Se o peso total da plataforma e dos contêineres é , determine a força compressiva em cada um dos dois pistões. O valor de depende da altura Que força é suportada por cada conexão, em seu ponto médio, quando está centrado entre e ?
Passo 1
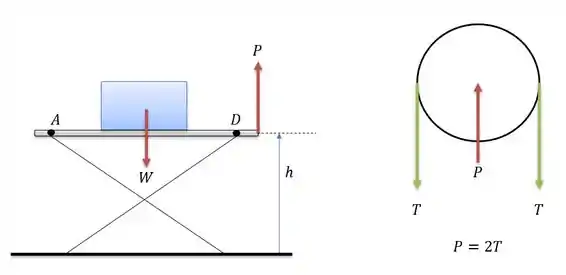
O enunciado fala de dois cilindros hidráulicos mas como cada polia se conecta a plataforma com um cabo valendo de força, logo a força que as duas polias farão na plataforma será de que é a mesma coisa que . Tal como pode ser vista na figura abaixo.
O que nos dá o seguinte sistema de forças para a polia e para a plataforma.
Fazendo a somatória dos trabalhos virtuais da plataforma nós teremos a seguinte equação:
Daria o mesmo resultado mas não estaria teoricamente correto fazer a somatória das forças ser zero, uma vez que temos as reações em e . Então para lidar somente com as forças externas temos que pensar sempre em trabalhos virtuais. E o valor de é independente de uma vez que as forças estão no mesmo plano.
Passo 2
Para encontrar a força no meio das conexões antes precisaremos saber as reações em e .
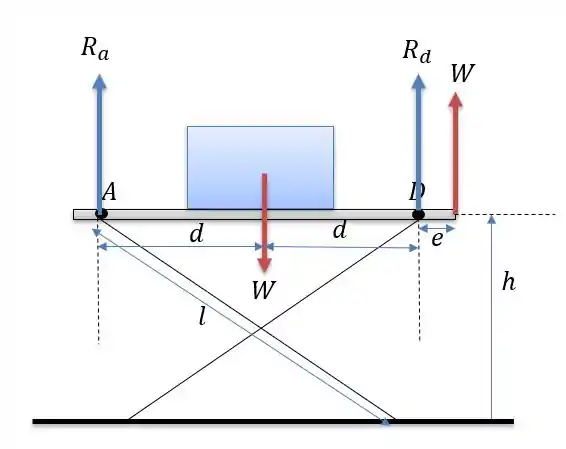
Onde chamamos de a distância das reações para o centro de massa da carga e ela pode ser calculada em relação as dimensões dadas no enunciada por Pitágoras, tal que:
Fazendo a somatória dos momentos em nós teremos:
Isolando :
Pela somatória das forças verticais podemos chegar na seguinte relação:
Logo:
Passo 3
Como existem duas conexões (como um na frente e um atrás, assim como para os cilindros hidráulicos ) teremos o seguinte sistema de forças para a barra .
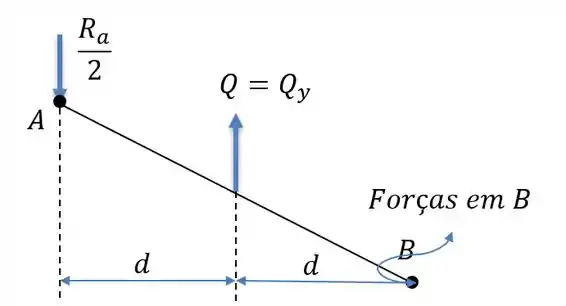
Onde em uma das conexões nós teremos uma força para baixo (para se opor as forças de cima e o sistema se manter estático) a metade do valor que encontramos e com apenas uma componente vertical no meio da conexão. Além de forças de reação em . Fazendo a somatória desses momentos no ponto nós teremos:
Resposta
Força independente de .