Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 54

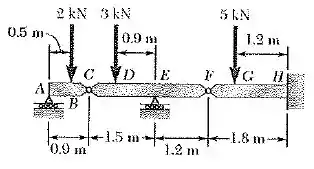
Usando o método do trabalho virtual, determine separadamente a força e o binário que representa a reação em H.

Passo 1

Primeiro vamos entender o problema! Temos forças verticais para baixo e por conta dessas forças vamos ter alguns deslocamentos, de tal modo que no ponto C vamos ter um deslocamento d y c , já no ponto F, vamos ter um deslocamento d y F , porém como FH se mantêm na horizontal podemos dizer que:

d y F = d y G = d y H

Certo, então vamos tirar algumas relações por semelhança de triângulo, observe a partir do ponto H, temos:

d y D = 0.9 1.2 d y F =   0.9 1.2 d y H = 0.75 d y H

Outra:

d y c = 1.5 0.9 d y D =   1.5 0.9 ( 0.75 d y H ) = 1.25 d y H

Outra:

d y B = 0.5 0.9 d y C =   0.5 0.9 ( 1.25 d y H ) = 0.69444 d y H

Passo 2

Agora que já achamos a relação dos deslocamentos, só basta utilizar o trabalho virtual que teremos nossa solução. De modo que o trabalho virtual é dado por:

d U = 2   k N d y b +   3   k N d y D - 5 k N d y G + H d y H

E como,

d U = 0

Então,

2   k N d y b +   3   k N d y D - 5 k N d y G + H d y H = 0

Passo 3

Já achamos a relação agora é só substituir com as relações que encontramos no Passo 1, então:

2   k N 0.69444 d y H +   3   k N 0.75 d y H - 5 k N d y H + H d y H = 0

Simplificando, teremos:

2   k N 0.69444 +   3   k N 0.75 - 5   + H = 0

Portanto,

H = 1.3611   k N

Passo 4

Do mesmo estilo que fizemos para o cálculo de H, vamos fazer para o cálculo do binário. A mudança é que vamos trabalhar com ângulos, ou seja, d θ . Que anteriormente assumimos que FH era na horizontal, porém agora vai ter uma inclinação d θ .  

Logo, note que:

d y g = 1.2 d θ e d y F = 1.8 d θ

Outra,

d y D = 0.9 1.2 d y F = 0.9 1.2 1.8 d θ = 1.35 d θ

Outra,

d y c = 1.5 0.9 d y D = 1.5 0.9 1.35 d θ = 2.25 d θ

Outra,

d y B = 0.5 0.9 d y C = 0.5 0.9 2.25 d θ = 1.25 d θ

Passo 5

Agora que já achamos a relação dos deslocamentos, só basta utilizar o trabalho virtual que teremos nossa solução. De modo que o trabalho virtual é dado por:

d U = 2   k N d y b +   3   k N d y D - 5 k N d y G + M H d θ

E como,

d U = 0

Então,

2   k N d y b +   3   k N d y D - 5 k N d y G + M H d θ = 0

Substituindo do Passo anterior teremos:

2   k N 1.25 d θ +   3   k N 1.35 d θ - 5 k N 1.2 d θ   + M H d θ = 0

Resolvendo encontraremos que:

M H =   - 0.550   k N * m

Resposta

H = 1.3611   k N

M H =   - 0.550   k N * m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método do trabalho virtual, determine a reação em E.
Determine o movimento vertical do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Dica: aplique uma carga vertical no nó D e, usando os métodos do Capítulo 6, calcule a força exercida pelo
Sabendo que o coeficiente de atrito estático entre o bloco preso à barra ACE e a superfície horizontal é igual a 0,15 , determine as intensidades da maior e da menor força Q para as quais o equilíbrio
Voltando ao Problema 10.45 e usando o valor encontrado para a força exercida pelo cilindro hidráulico BD, determine a mudança no comprimento de BD necessária para se elevar a plataforma presa em C em
Representado por μ s , o coeficiente de atrito estático entre o colar C e a haste vertical, deduza uma expressão para a intensidade do maior binánrio M para o qual o equilíbrio é mantido na posição mo