Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 12
Se e , determine o momento resultante produzido por essas forças em relação ao ponto . Expresse o resultado como um vetor cartesiano.
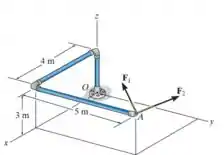
Passo 1
Para determinar o momento resultante das forças, é necessário determinar apenas a força resultante na forma de vetor cartesiano e o vetor posição . Assim, será possível determinar o momento gerado a partir do produto vetorial
Passo 2
Logo, a força resultante é dada por:
O vetor posição é:
Passo 3
Por fim, o momento será:
Resposta
Exercícios de Livros Relacionados
Determine a intensidade e os ângulos de direção coordenados da força resultante que age sobre A .
O lustre é sustentado por três corrente que são concorrentes no ponto O . Se a força em cada corrente possui uma intensidade de 300 N , expresse cada força como um vetor cartesiano e determine a inten
O lustre é sustentado por três correntes que são concorrentes no ponto O . Se a força resultante em O possui uma intensidade de 650N e é direcionada ao longo do eixo z positivo, determine a força em c
A torre de antena é sustentada por três cabos. Se as forças desses cabos que atuam sobre a antena são F B = 520 N, F C = 680 N e F D = 560 N, determine a intensidade e os ângulos de direção coordenado
O cabo A O exerce uma força sobre o topo do poste de F = { - 120 i - 90 j - 80 k } N. Se o cabo possui um comprimento de 1,02 m, determine a altura z do poste e a posição ( x ,y ) de sua base.