Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas de Revisão - Ex. 70

I = 100 m m   e   F = 5 k N ,   determine as tensões normal e de cisalhamento no a no ponto H , b ponto K.

Passo 1

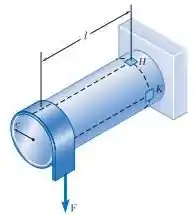
E ai gurizada tudo beleza? O enunciado pede que a gente determine as tensões normal e de cisalhamento no a no ponto H , b ponto K. Então vamos ao esboço ;)

Passo 2

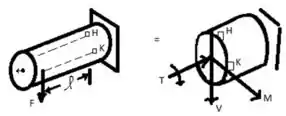
Agora vamos continuar , vem comigo :D

Na seção contendo ponto H e K,

T = F c     M = F I     V = F

J = π 2 c 4       I = π 4 c 4

Ponto H:

σ = M c I = F l c π 4 c 4         σ = 4 F l π c 2

τ = T c J = F c 2 π 4 c 4 τ = 2 F π c 2

Ponto K: Ponto K no eixo neutro σ = 0

Por causa do torque:

τ = T c J = 2 F π c 2

Por causa do cisalhamento: Para um semicírculo

Q = 2 3 c 3 ,   t = d = 2 c

τ = V Q I t = F 2 3 c 3 π 4 c 4 ( 2 c ) = 4 F 3 π c 2

Combinados:

τ = 2 F π c 2 + 4 F 3 π c 2             τ = 10 F 3 π c 2

Passo 3

Então vamos considerar os dados:

: F = 5 k N = 5 × 10 3 N ,             l = 100 m m = 0,100 m c = 20 m m = 0,020 m

  1. Ponto H: σ = 4 5 x 10 3 0,100 π 0,020 3                                               σ = 79,6 M P a

    2. τ = 2 5 x 10 3 π 0,020 2                                 τ = 7,96 M P a

  2. Ponto K:

τ = 10 5 × 10 3 3 π 0,020 2                                                   τ = 13,26 M P a

Resposta

  1. τ = 7,96 M P a
  2. τ = 13,26 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força vertical P de intensidade 60lb é aplicada no ponto A da manivela. Sabendo que o eixo BDE tem um diâmetro de 0,75in., determine as tensões principais e a tensão de cisalhamento máxima no ponto
Resolva o Problema 8,45 considerando que h =304,8mm
Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos princip
(8.49)Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos p
8,47:(Três forças são aplicadas à barra mostrada na figura. Determine as tensões normal e de cisalhamento (a) no ponto a, (b) no ponto b e (c) no ponto c.) Resolva o problema 8.47 considerando que for