Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 50

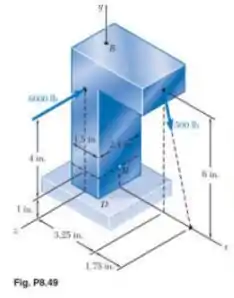
(8.49)Duas forças são aplicadas a uma pequena coluna BD conforme mostrado. Sabendo que a porção vertical da coluna tem uma seção transversal de 1,5x2,4in., determine as tensões principais, os planos principais e a máxima tensão de cisalhamento no ponto H.

8.50: Resolva o Prob. 8.49, assumindo que a intensidade da força de 6000lb é reduzida para 1500lb

Passo 1

Componentes da força de 500-lb:

F x = 500 1,75 6,25 = 140 l b

F y = - 500 6 6,25 = - 480 l b

Braço de momento da força de 500-lb:

r → = 3,25 i → + ( 6 - 1 ) j →

Momento da força de 500-lb:

M → = i → j → k → 3,25 5 0 140 - 480 0 = - 2260 k → l b ∙ i n .

Passo 2

Na seção contando o ponto H, P = - 480 l b           V x = 140 l b

V z = - 1500 l b ,     M z = - 2260 l b ∙ i n . ,     M x = - 4 1500 = - 6000 l b ∙ i n .

A = 1,5 2,4 = 3,6 i n 2     I z = 1 12 2,4 1,5 3 = 0,675 i n 4

σ H = P A + M z x I z = - 480 3,6 + - 2260 0,75 0,675 = - 2644 p s i

τ H = 3 2 V z A = 3 2 1500 3,6 = 625 p s i

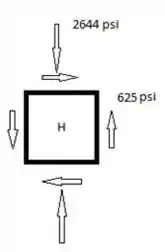
Passo 3

Usando círculo de Mohr

σ a v e = - 2644 2 = - 1322 p s i

R = 2644 2 2 + 625 2 = 1462,30 p s i

σ a = σ a v e + R         σ = 140,3 p s i  

    σ b = σ a v e - R                 σ b = - 2780 p s i

t a n 20 p = 2 τ H σ H = 2 625 2644 = 0,4728

θ a = 12,6 ° ,             θ b = 102,6 °

τ M A X = R                                 τ M A X = 1462 p s i

Resposta

625 p s i

1462 p s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a
β = 0) e com seu eixo longitudinal AB horizontal, determine a intensidade da força P para a qual a tensão normal no ponto a é +120Mpa, (b) Resolva a parte a considerando que a viga é instalado com β =
Quatro forças são aplicadas a um perfil de aço laminado W8 x 28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto b.
P 1 e P 2 são aplicadas, como mostrado na figura, em direções perpendiculares ao eixo longitudinal de uma viga W310x60. Sabendo que P 1 = 25 k N e P 2 = 24 k N , determine as tenções principais e a te
Desprezando o efeito dos adoçamentos e das concentrações de tensões, determine os menores diâmetros permissíveis para as hastes sólidas BC e CD. Utilize T a d m = 60 M P a .