Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 105

101- Determine as reações em A e B para a viga submetida a uma combinação de cargas distribuída e concentrada.

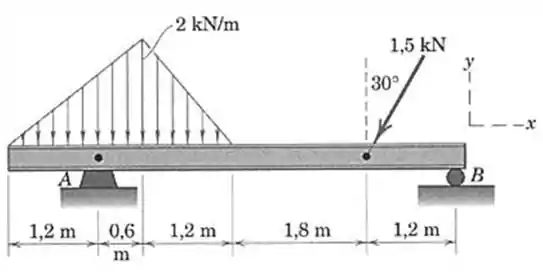
Passo 1

As cargas nas vigas podem ser escritas da seguinte forma:

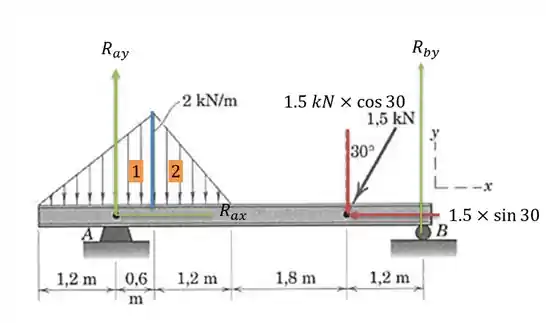
Onde o suporte A apresenta reação horizontal e vertical.

Passo 2

A área 1 contribui com uma força igual a:

F 1 = 2 k N m × 1.2 + 0.6 2 = 1.8   k N

E essa força atua na posição da barra:

x 1 - = 1.2 + 0.6 × 2 3 = 1.2   m

E a área 2 contribui com uma força igual a:

F 2 = 2   k N / m × 1.2   m 2 = 1.2   k N

E está na posição da viga igual a:

x - 2 = 1.8 m + 1.2 m 3 = 2.2   m

Além de que a carga pontual contribui horizontalmente com:

1.5   k N × sin ⁡ 30 = 0.75   k N

E verticalmente igual a:

1.5   k N × cos ⁡ 30 = 1.3   k N

Passo 3

Isso faz com que nossa viga fique com a seguinte característica:

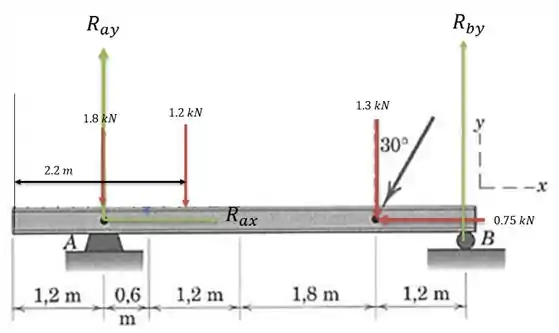
Fazendo a soma das forças horizontais iguais a zero nos dá:

R a x = 0.75   k N

Fazendo a soma das forças verticais ser 0 nos dá:

R a y + R b y = 1.8   k N + 1.3   k N + 1.2   k N = 4.3   k N

Agora fazendo a somatória dos momentos em A   ser 0 fazendo o sentido horário ser positivo. Atente-se pois precisamos calcular as distâncias das forças para o ponto A e que forças que estão paralelas a essa distância não causam nenhum momento, somente as perpendiculares.

1.8   k N × 0 + 1.2   k N × 2.2 - 1.2 m + 1.3   k N × 3.6   k N - R b y × 4.8 m = 0

R b y = 1.225   k N

O que nos dá a reação vertical em A igual a:

R a y = 4.3 k N - 1.225 = 3.075   k N

Resposta

R a x = 0.75   k N

R a y = 3.075   k N

R b y = 1.225   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força resultante e especifique onde ela atua na viga, medindo a partir do ponto A .
O carregamento distribuído atua sobre a viga conforme ilustrado. Determine a intensidade da força resultante equivalente e especifique onde ela age, medindo a partir do ponto A .
O carregamento distribuído atua sobre a viga conforme ilustrado. Determine a intensidade máxima w m á x á . Qual é a intensidade da força resultante equivalente? Especifique onde ela atua, medindo a p
O letreiro triangular está preso ao poste engastado em uma base de concreto em B . Calcule a força cisalhante V , o momento fletor M e o momento torçor T sobre o poste em B , durante uma tempestade na
Uma placa plana sela uma abertura triangular na parede vertical de um tanque com líquido de massa específica ρ . A placa bascula em torno da borda superior O do triângulo. Determine a força P necessár