Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 10
- Por meio de um mecanismo de cremalheira e pinhão, grandes forças podem ser desenvolvidas pelo saca rolhas mostrado. Se o raio médio das engrenagens do pinhão vale , determine a força que é exercida sobre a rolha para as forças dadas, , nas manoplas.
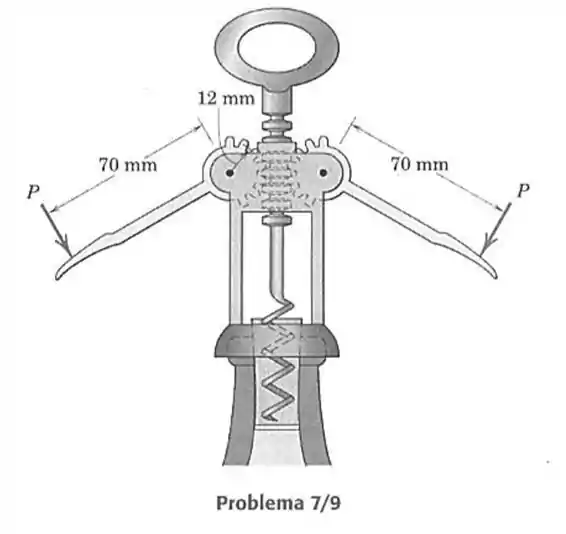
Passo 1
Vamos representar o sistema da seguinte forma.
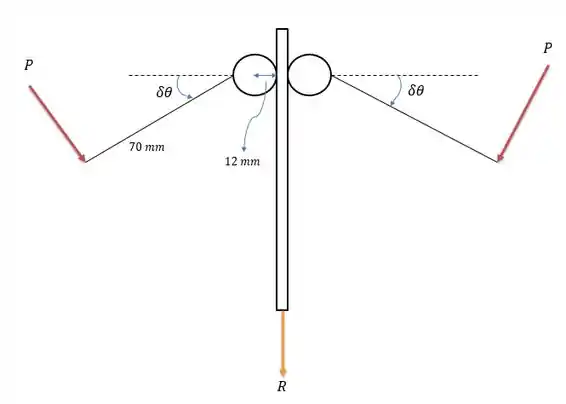
Onde as duas forças se pressionadas com a mesma intensidade tendem a fazer com que as duas engrenagens tendam a subir contribuindo com um trabalho virtual total igual a:
E a força de ação contribui com para as duas engrenagens para que elas façam caminho contrário ao estipulado no desenho, tendo o seu trabalho virtual calculado da seguinte forma:
Passo 2
Calculando a somatória dos trabalhos virtuais do mecanismo nós teremos:
Cortando temos:
Resposta
Exercícios de Livros Relacionados
Resolva o problema 10.39 considerando que P=350 N , l = 250m m e K = 12,5N ⋅ m / r a d . Obtenha as respostas para cada um dos seguintes quadrantes: 0θ90 ° ,27 0 °θ36 0 ° , 36 0 °θ45 0 ° .
A posição da manivela ABC é controlada pelo cilindro hidráulico BD. Para o carregamento mostrado na figura, determine a força exercidad pelo cilindro hidráulico no pino B, sabendo que θ = 65 ° .
A posição da manivela ABC é controlada pelo cilindro hidráulico CD. Para o carregamento mostrado na figura, determine a força exercida pelo cilindro hidráulico no pino C quando θ = 55 ° .
A posição da manivela ABC é controlada pelo cilindro hidráulico CD. Determine o ângulo θ sabendo que o cilindro hidráulico exerce uma força de 15 k N no pino C.
O braço telescópico ABC é usado para prover uma plataforma elevada para operários construção. Juntos, operários e a plataforma têm um peso de 2250N , e seu centro de gravidade está localizado diretame