Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 238
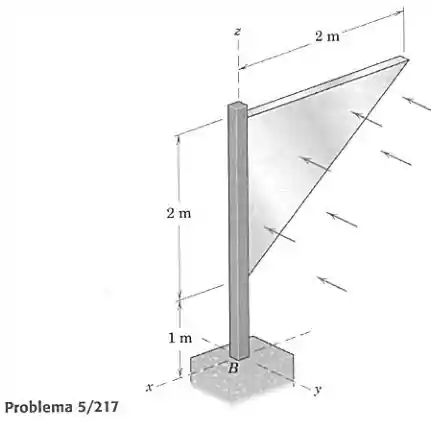
O letreiro triangular está preso ao poste engastado em uma base de concreto em . Calcule a força cisalhante , o momento fletor e o momento torçor sobre o poste em , durante uma tempestade na qual a velocidade do vento normal ao letreiro atinge 100 km/h. A pressão do ar (chamada pressão de estagnação) contra a superfície vertical, correspondente a esta velocidade, vale 1,4 kPa.
Passo 1
A força causada pela pressão do vento será aplicada no centroide da região triangular do letreiro. Essa força será a nossa força cisalhante . A partir disso, vamos calcular o momento causado em relação ao eixo , que será o momento torçor , o momento causado em relação ao eixo , que será o momento fletor .
Passo 2
Primeiro vamos calcular o valor da força causada pelo vento. Temos uma pressão de 1,4 kPa, e uma área dada por:
Então achamos o valor da força:
O resultado está em kN pois multiplicamos a área por kPa. Sabemos que a força cisalhante será igual à força causada pelo vento. Então:
Passo 3
Precisamos agora calcular o momento fletor . Esse é o momento que tenta fazer a força girar em torno do eixo . Sabemos que o centroide de um triângulo que possui uma altura em relação a uma base fica a uma distância até essaa base de . Então achamos o centroide da área triangular facilmente, tendo como bases os catetos:
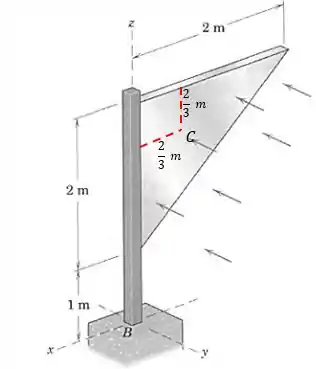
Temos então para a força aplicada um braço de alavanca em relação ao eixo de . Então:
Passo 4
Agora calculamos o momento torçor , que faz a viga girar em torno do próprio eixo, o eixo . Temos um braço de alavanca de , então: