Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 1
Sabendo-se que a mola em A é de constante k e que a barra AB é rígida, determinar a carga crítica PCR
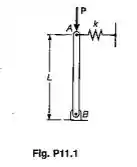
Passo 1
Faala galerinha, bora fazer um exercício de carga crítica?
Aqui nossa meta é achar a carga crítica, ou seja que faz a nossa coluna flambar. Vamos começar fazendo um diagrama de corpo livre da coluna e imaginar o que acontece quando a gente coloca aquela força ali.
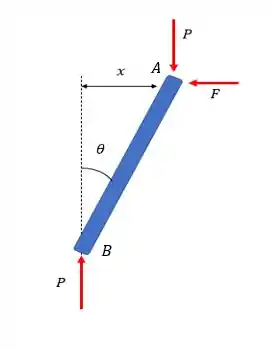
Repare que ao aplicarmos o peso, a barra vai se deslocar e a mola vai reagir no sentido contrário ao deslocamento com a força F. E vai aparecer pra gente um ângulo mostrando o quanto a barra foi girada.
Lembrando que a força de uma mola é dada por:
A nossa meta aqui é relacionar a força P com a força causada pela mola.
Passo 2
Vamos começar a eliminar as incógnitas, nós vimos esse x e dá pra colocar ele em função da geometria olhando para o triângulo da figura:
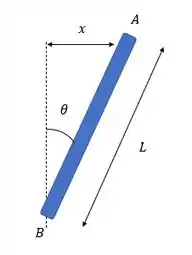
Daqui a gente tira que:
E então:
E se a gente fizer o somatório dos momentos no ponto B, a gente vai ter considerando o sentido horário positivo:
Substituindo x e F.
E aqui vai o bizu da questão, esse tipo de ângulo é beeeeeem pequeno quase zero graus então a gente pode dizer que:
E:
E aí substituindo:
Isolando P a gente vai ter:
Enfim temos a nossa carga, é isso!