Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 42

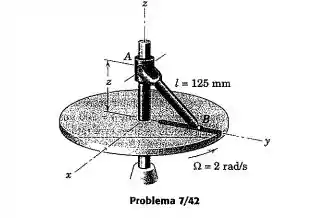
O cursos e o garfo A recebem uma velocidade ascendente constante de 0,2   m / s durante um intervalo de movimento e obrigam a esfera na extremidade da barra a deslizar na ranhura radial no disco em rotação. Determine a aceleração angular da barra no instante em que a barra passa pela posição em que z = 75   m m . O disco gira à taxa constante de 2   r a d / s .

Passo 1

Para resolvermos esse problema usaremos as relações de aceleração relativa entre os eixos além de relações das funções horários do movimento.

Passo 2

Vamos começar chamando o ângulo onde B está em contato com o disco de um ângulo β . Sendo assim a velocidade angular de todo o sistema será:

ω = - β ˙ ⋅ i ^ + Ω ⋅ k ^

E para a aceleração:

α = ω ˙ = - β ¨ ⋅ i ^ - β ˙ ⋅ i ^ ˙ + 0 = - β ¨ ⋅ i ^ - β ˙ ⋅ ( Ω × i ^ )

Mas, temos também que z = l ⋅ s e n β . Como queremos o ponto onde z = 0.075   m , temos que o ângulo nesse momento será de β = a r c s e n l z = 0.64   r a d .

Temos, derivando a relação acima, que a velocidade em que a barra se desloca até essa posição será:

z ˙ = l ⋅ β ˙ ⋅ cos ⁡ β

E a velocidade pode ser obtida através da relação de Torricelli. Assim, temos que a velocidade até o ponto em que z = 0.075 m será:

z ˙ f = z ˙ i - 2 ⋅ z ¨ ⋅ Δ z = 0.2   m / s

Onde z ¨ = 0.2   m / s , z ˙ i = 0 e Δ z = - 0.05   m . Assim, temos que nosso β ˙ é dado da seguinte forma:

β ˙ = z ˙ l ⋅ cos ⁡ β = 2   r a d / s

Para obtermos β ¨ , basta derivarmos z ˙ . Assim, ficamos com:

z ¨ = 0 = - l ⋅ β ˙ 2 ⋅ s e n β + l ⋅ β ¨ ⋅ cos ⁡ β

β ¨ = β ˙ 2 ⋅ t g β = 3   r a d / s 2

Substituindo os valores agora na equação de α , temos que:

α = - β ¨ ⋅ i ^ - β ˙ ⋅ Ω × i ^ = - 3   r a d / s 2 ⋅ i ^ - 2   r a d / s ⋅ 2 r a d / s ⋅ j ^ = - 3 ⋅ i ^ - 4 ⋅ j ^   r a d / s 2

Resposta

Resposta: α = - 3 ⋅ i ^ - 4 ⋅ j ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco circular de 120 mm de raio gira em torno do eixo z na taxa constante de w = 20 rad/s, e o conjunto inteiro gira em torno do eixo fixo x na taxa constante wx = 10 rad/s. Calcule os módulos da v
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine as expressões para a velocidade v e a acel
A extremidade do elemento de ligação A está soldada ao garfo que é articulado em relação ao eixo z ao cursor C. O cursor pode girar em torno do eixo x da barra fixa. O elemento de ligação A e seu garf
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine a expressão vetorial para a aceleração ang