Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 106
106. As pás e o cubo do rotor do helicóptero têm uma massa de e um raio de giração de em relação ao eixo de rotação . Com o rotor girando a durante um curto intervalo após a decolagem vertical o helicóptero se inclina para frente à taxa para adquirir velocidade para a frente. Determine o momento giroscópico transmitido ao corpo do helicóptero por seu rotor e indique se o helicóptero tende a se desviar no sentido horário ou anti-horário, quando visto por um passageiro olhando para a frente.
Passo 1
Primeiramente vamos definir o quanto vale o nosso giro . Olho lá, que a questão nos forneceu a velocidade em . Para converter para , basta dividir tudo por e encontramos o que queremos:
E agora, bora tratar de descobrir o valor da precessão, dado que o helicóptero se inclina para frente à taxa , ou seja:
E por último, falta determinar o momento de inércia do noss sistema. Para isso, basta multiplicar a massa do nosso sistema (pás e cubo do rotor) pelo seu respectivo raio de giração ao quadrado:
Passo 2
Obtido, o momento de inércia , a velocidade de giro e o valor da precessão , bora tratar de obter o momento através da fórmula que todo mundo já tá careca de saber:
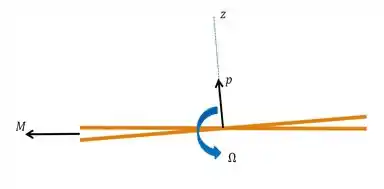
E bora agora, tentar representa a vista frontal do helicóptero de acordo com o observado e contendo também o momento que nele está agindo. Ignore o desastre que é essa imagem e pense apenas no momento.
Desse modo temos que o nosso helicóptero tende a se desviar no sentido anti-horário, quando visto por um passageiro olhando para a frente
Resposta
O helicóptero tende a se desviar no sentido anti-horário, quando visto por um passageiro olhando para a frente.